Questões sobre Cilindro | Pratique com o Prisma

638c7427-7a

ENEM 2021 - Matemática - Geometria Espacial, Cilindro

Um povoado com 100 habitantes está passando poruma situação de seca prolongada e os responsáveispela administração pública local decidem contratar aconstrução de um reservatório. Ele deverá ter a formade um cilindro circular reto, cuja base tenha 5 metrosde diâmetro interno, e atender à demanda de água dapopulação por um período de exatamente sete diasconsecutivos. No oitavo dia, o reservatório vazio écompletamente reabastecido por carros-pipa.

Considere que o consumo médio diário por habitanteé de 120 litros de água. Use 3 como aproximação para π.

Nas condições apresentadas, o reservatório deverá serconstruído com uma altura interna mínima, em metro, igual a

A

1,12.

B

3,10.

C

4,35.

D

4,48.

E

5,60.

3218a147-57

ENEM 2021 - Matemática - Geometria Espacial, Cilindro

Um povoado com 100 habitantes está passando por uma situação de seca prolongada e os responsáveis pela administração pública local decidem contratar a construção de um reservatório. Ele deverá ter a forma de um cilindro circular reto, cuja base tenha 5 metros de diâmetro interno, e atender à demanda de água da população por um período de exatamente sete dias consecutivos. No oitavo dia, o reservatório vazio é completamente reabastecido por carros-pipa.

Considere que o consumo médio diário por habitante é de 120 litros de água. Use 3 como aproximação para π .

Nas condições apresentadas, o reservatório deverá ser construído com uma altura interna mínima, em metro, igual a

A

1,12.

B

3,10.

C

4,35.

D

4,48.

E

5,60.

23fd1708-04

CEDERJ 2021 - Matemática - Geometria Espacial, Cilindro

Um reservatório de água tem a forma de um cilindro circular reto de altura 2,5 metros e raio 4 metros. Para calcular o volume desse reservatório, em metros cúbicos, deve-se multiplicar o número π pela expressão

A

2,5² + 4.

B

2,5 + 4².

C

2,5² x 4.

D

2,5 x 4².

9451a72b-05

UFRGS 2016 - Matemática - Geometria Espacial, Cilindro

Em uma caixa, há sólidos geométricos, todos de mesma altura: cubos, cilindros, pirâmides quadrangulares regulares e cones. Sabe-se que as arestas da base dos cubos e das pirâmides têm a mesma medida; que o raio da base dos cones e dos cilindros tem a mesma medida. Somando o volume de 2 cubos e de 2 cilindros, obtêm-se 180 cm³ . A soma dos volumes de 3 cubos e 1 cone resulta em 110 cm³ , e a soma dos volumes de 2 cilindros e 3 pirâmides resulta em 150 cm³.

O valor da soma dos volumes, em cm³ , de um cubo, um cilindro, dois cones e duas pirâmides é

A

150.

B

160.

C

190.

D

210.

E

240.

9aee80cb-07

UNICENTRO 2015 - Matemática - Geometria Espacial, Cilindro

Assinale a alternativa que apresenta, corretamente, o volume da semiesfera.

Leia o texto a seguir e responda à questão.

A figura a seguir representa um modelo geométrico de um pilar de concreto, onde são usadas correntes fixas para um sistema de segurança.

O modelo representado na figura é um sólido com volume de 90π dm3 , que pode ser decomposto em um cilindro reto e uma semiesfera, cujos raios são iguais a 3 dm.

A

18π

B

24π

C

36π

D

40π

E

60π

9aeaf383-07

UNICENTRO 2015 - Matemática - Sistema de Unidade de Medidas, Aritmética e Problemas, Geometria Espacial, Cilindro

Com base nessa figura, assinale a alternativa que apresenta, corretamente, a altura desse sólido.

Leia o texto a seguir e responda à questão.

A figura a seguir representa um modelo geométrico de um pilar de concreto, onde são usadas correntes fixas para um sistema de segurança.

O modelo representado na figura é um sólido com volume de 90π dm3 , que pode ser decomposto em um cilindro reto e uma semiesfera, cujos raios são iguais a 3 dm.

A

6 dm

B

8 dm

C

9 dm

D

11 dm

E

12 dm

620923d5-ff

URCA 2017 - Matemática - Geometria Espacial, Cilindro

Um cone e um cilindro circulares retos têm uma base comum e o vértice do cone se encontra no centro da outra base do cilindro. Se o raio da base mede 2cm e a área total do cone mede 4π(√17+1)cm². Calcule o volume do cilindro.

A

32π cm3

B

40√17π cm3

C

42π cm3

D

64√17π cm3

E

16√17 π cm3

cb7ed16f-02

MACKENZIE 2019 - Matemática - Geometria Espacial, Cilindro

Em um recipiente cilíndrico de raio 6 cm e altura 9 cm, completamente cheio de água, foi colocada uma esfera metálica. Assim, observou-se que a esfera ficou totalmente submersa na água, transbordando 36 π cm3 de água. Então, o raio da esfera, em cm, mede

A

2

B

3

C

4

D

5

E

6

af727e2b-ff

URCA 2016 - Matemática - Geometria Espacial, Cilindro

Se girarmos um retângulo em torno do seu lado maior, teremos um cilindro de volume igual a 375πcm3. Sabendo que o lado maior do retângulo mede o triplo do lado menor, então a razão entre a sua área e o seu perímetro é igual a:

A

5

B

15

C

15/3

D

5/8

E

15/8

50484dc5-f7

UNEMAT 2016 - Matemática - Geometria Espacial, Cilindro

Um açucareiro com formato cilíndrico tem uma tampa circular cujo raio mede 5 cm. A tampa possui um dispositivo que abre em “V” e o arco formado pela abertura máxima do ângulo mede 1 radiano, conforme apresentado na figura.

Qual a área máxima de abertura desse açucareiro?

A

12,5 cm²

B

19,6 cm²

C

15,7cm²

D

31,4 cm²

E

17,2 cm²

4baa2bb3-8f

UNICAMP 2021 - Matemática - Circunferências e Círculos, Geometria Plana, Geometria Espacial, Cilindro

No início do expediente do dia 16 de março de 2020, uma farmácia colocou à disposição dos clientes um frasco cilíndrico de 500 ml (500 cm²) de álcool em gel para higienização das mãos. No final do expediente, a coluna de álcool havia baixado 5 cm. Sabendo que a base do cilindro tem diâmetro de 6 cm e admitindo o mesmo consumo de álcool em gel nos dias seguintes, calcula-se que o frasco ficou vazio no dia

A

17 de março.

B

18 de março.

C

19 de março.

D

20 de março.

eb2789c3-7f

IMT - SP 2020 - Matemática - Geometria Espacial, Cilindro

Considere um cilindro circular reto de altura H = 4 m e um tetraedro, cuja base é o triângulo ABC inscrito no semicírculo como mostra a figura. Sabe-se que e que o volume do tetraedro é 1/3 do volume do cilindro. Nessas condições, a altura h do tetraedro, em metros, é

A

B

C

D

E

68f5749d-7c

ENEM 2020 - Matemática - Geometria Espacial, Cilindro

Um piscicultor cria uma espécie de peixe em um tanque cilíndrico. Devido às características dessa espécie, o tanque deve ter, exatamente,2 metros de profundidade e ser dimensionado de forma a comportar 5 peixes para cada metro cúbico de água. Atualmente, o tanque comporta um total de 750 peixes. O piscicultor deseja aumentara capacidade do tanque para que ele comporte900 peixes, mas sem alterar a sua profundidade. Considere 3 como aproximação para π.

O aumento da medida do raio do tanque, em metro, deve ser de

A

√30 − 5

B

C

√5

D

5/2

E

15/2

36c8a697-6a

URCA 2021 - Matemática - Aritmética e Problemas, Áreas e Perímetros, Geometria Plana, Frações e Números Decimais, Geometria Espacial, Cilindro

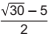
Em um cilindro circular reto de altura 1 m, sabe-se que a razão entre a área lateral e a área total é 1/3 . Qual o valor do raio da base?

A

1 m

B

2 m

C

3 m

D

4 m

E

5 m

9f0a5998-5f

ENEM 2020 - Matemática - Geometria Espacial, Cilindro

Uma loja de materiais de construção vende dois tipos de caixas-d’água: tipo A e tipo B. Ambas têm formato cilíndrico e possuem o mesmo volume, e a altura da caixa-d’água do tipo B é igual a 25% da altura da caixa-d’agua do tipo A.

Se R denota o raio da caixa-d’água do tipo A, então o raio da caixa-d'água do tipo B é

A

R/2

B

2 R

C

4 R

D

5 R

E

16 R

c30222f7-fd

UNC 2011 - Matemática - Sistema de Unidade de Medidas, Aritmética e Problemas, Geometria Espacial, Cilindro

Um posto de combustíveis abastece mensalmente seu reservatório cilíndrico subterrâneo, cujas medidas estão indicadas no esquema a seguir.

Considerando que o reservatório esteja vazio e que será abastecido com 80% de sua capacidade por um caminhão tanque, a uma vazão de 10 L por segundo, em aproximadamente quantos minutos o reservatório será abastecido?

A

59 min.

B

51 min.

C

47 min.

D

48 min.

f75689cf-fc

FUVEST 2019 - Matemática - Geometria Espacial, Cilindro

O cilindro de papelão central de uma fita crepe tem raio externo de 3 cm. A fita tem espessura de 0,01 cm e dá 100 voltas completas. Considerando que, a cada volta, o raio externo do rolo é aumentado no valor da espessura da fita, o comprimento total da fita é de, aproximadamente,
Note e adote:
π = 3,14.

A

9,4 m.

B

11,0 m.

C

18,8 m.

D

22,0 m.

E

25,1 m.

4d0edb89-ff

UNICENTRO 2019 - Matemática - Geometria Espacial, Cilindro, Poliedros

Uma fábrica de azeite deseja mudar a sua embalagem de cilíndrica para um prisma quadrangular, como mostra o esquema.

De acordo com a figura, a altura do prisma deve ser igual a

A

π

B

2π

C

2,5 π

D

3 π

019f4100-fd

MULTIVIX 2019 - Matemática - Geometria Espacial, Cilindro

Três canos de forma cilíndrica e de mesmo raio r, estão dispostos como na figura abaixo:
É possível encaixar os três canos de forma que fiquem presos e sem folga dentro de um cilindro maior de raio R. Qual das alternativas a seguir expressa o valor de R em função de r para que isto seja possível?

A

R= 2r √3 / 2 + r

B

R= 2r√3 / 3

C

R= 2r√3 / 4 + r

D

R= 2r√3 / 3+ √3

E

R= 2r√3 / 3 + 1

be89c200-fe

UNICENTRO 2019 - Matemática - Geometria Espacial, Cilindro

Em um trecho de 6m de uma tubulação, cujo diâmetro externo é de 4,6m, cabem cerca de 40,5m³ de água.
Usando-se π ≅ 3, se preciso, é correto estimar que a espessura E, em metros, da parede dessa tubulação é de, aproximadamente,

A

0,2

B

0,3

C

0,8

D

1,5

E

2,0

Questõessobre Cilindro