fb91326b-e1
CEDERJ 2016 - Matemática - Potenciação, Álgebra, Problemas
Se 320 = 5.20,03t
, então o valor de t é igual a:
Se 320 = 5.20,03t
, então o valor de t é igual a:
A
2.10²
B
2.10⁻²
C
2.10³
D
2.10⁻³
O número 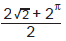 pertence ao intervalo:
pertence ao intervalo:
Se f e g são funções reais definidas por 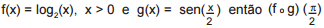 é igual a
é igual a
A tabela abaixo exibe as notas em quatro provas P1 , P2 ,P3 e P4 , de quatro alunos denominados por X, Y, Z e W.
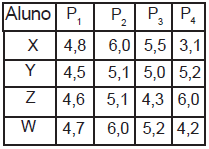
A menor mediana das quatro provas é a do aluno

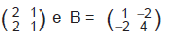 é a matriz nula de ordem 2.
é a matriz nula de ordem 2.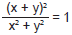 .
.
 é igual a:
é igual a:
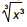 = x, para todo x ∈ IR.
= x, para todo x ∈ IR.