Questõesde CEDERJ sobre Matemática

InícioTodas as questões
1
1
Foram encontradas 123 questões
72554558-b0
CEDERJ 2019, CEDERJ 2019 - Matemática - Seno, Cosseno e Tangente, Trigonometria

O menor número real positivo que satisfaz a equação 2cosx - 1 = 0 é:

A
π/6
B
π/4
C
π/3
D
π/2
72447303-b0
CEDERJ 2019, CEDERJ 2019 - Matemática - Álgebra, Problemas

Pelas normas estabelecidas no Edital de um concurso para professores, seriam eliminados apenas os candidatos que tirassem nota zero em Matemática ou em Redação. Em tal concurso, 210 candidatos foram eliminados, sendo que 180 candidatos tiraram nota zero em Matemática e 90 candidatos tiraram zero em Redação.

O número de candidatos que tiraram nota zero apenas em Matemática é igual a:

A
120
B
90
C
60
D
30
5a7cb31b-af
CEDERJ 2011, CEDERJ 2011 - Matemática - Probabilidade, Álgebra, Equação do 2º Grau e Problemas do 2º Grau, Matrizes, Álgebra Linear

Assinale a afirmativa VERDADEIRA.

A
Se a e b são números reais tais que a < b, então a2 < b2
B
Não existe x ∈ IR , 0 < x < 2π, de modo que a  secante de x seja igual a 1/5
C
Se A e B são matrizes quadradas de mesma ordem, então AB = BA.
D
Se um número inteiro é escolhido ao acaso no conjunto { k ∈ Z tal que 0 < k < 100}, então a probabilidade de que esse número seja par é igual a 50%.
5a839915-af
CEDERJ 2011, CEDERJ 2011 - Matemática - Análise de Tabelas e Gráficos

Após se encher um determinado recipiente com água, construiu-se o gráfico abaixo, formado pela justaposição de dois segmentos de reta com inclinações diferentes, o qual indica a altura do nível da água em função do volume no recipiente.



Considere esse gráfico e indique qual é o formato do recipiente correspondente a ele.

A

Dois troncos de cones circulares retos

B

Um tronco de cone circular reto

C

Dois cilindros circulares retos

D

Um cilindro circular reto

5a7fdacc-af
CEDERJ 2011, CEDERJ 2011 - Matemática - Áreas e Perímetros, Geometria Plana

O ponto (0,2) pertence ao círculo cujo centro é o ponto (-1, 1). − A área de um quadrado que pode ser inscrito em tal círculo é igual a

A
1
B
√2
C
4
D
√10
5a78c794-af
CEDERJ 2011, CEDERJ 2011 - Matemática - Aritmética e Problemas, Álgebra, Porcentagem, Equação do 2º Grau e Problemas do 2º Grau, Geometria Plana, Triângulos

Assinale a afirmativa FALSA.

A

Se x é a medida, em radianos, de um ângulo e se , então, necessariamente, sen(x) < 0.

B
Se o preço de um certo produto aumenta 2% ao ano, então os valores desse produto, a cada ano, formam uma progressão geométrica de razão q = 1 + 2/100 .
C
Se a é um número real e se x2 + x + 2 > a para todo x ∈ IR, então a < 7/4.
D
Não é possível construir um triângulo cujos lados medem 2 cm, 3 cm e 6 cm.
5a733e81-af
CEDERJ 2011, CEDERJ 2011 - Matemática - Álgebra, Radiciação

Se 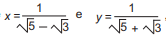, então é correto afirmar que x - y é igual a

A

B

C

D

710d97b1-8b
CEDERJ 2019 - Matemática - Álgebra Linear - Equações Lineares, Espaço Vetorial e Transformações Lineares e Matrizes, Álgebra Linear

Sobre sistemas de equações lineares 3 x 3, é verdadeiro que

A
todo sistema de equações lineares 3 x 3 possui pelo menos uma solução.
B
existe um sistema de equações lineares 3 x 3 que possui exatamente duas soluções distintas.
C
não existe um sistema de equações lineares 3 x 3 que possui infinitas soluções distintas.
D
se um sistema de equações lineares 3 x 3 possui pelo menos duas soluções distintas, então ele possui infinitas soluções distintas.
7109afff-8b
CEDERJ 2019 - Matemática - Funções, Função de 1º Grau, Função de 2º Grau

Abaixo são feitas afirmações sobre funções reais. Identifique a verdadeira.

A

Para x > 1, a função é a inversa da função

B
Para todos os números reais x e y, tem-se exy = ex ey.
C

O domínio da função real é um intervalo.

D
Para x > 0, a função definida por f(x) = In|x| é igual à função g(x) = |In(x)|.
70fc3865-8b
CEDERJ 2019 - Matemática - Relações Trigonométricas no Triângulo Retângulo, Leis dos Senos e Cossenos., Geometria Plana, Triângulos

A respeito de um triângulo retângulo cuja medida da hipotenusa é a e cujos catetos medem, na mesma unidade de comprimento, b e c, considere as três afirmações:


I Sendo T1 , T2 e T3 triângulos equiláteros de perímetros 3 a, 3 b e 3 c , respectivamente, a área de T1 é igual à soma das áreas de T2 e T3 .

II A área de um círculo, C1 , de raio com medida a é igual à soma das áreas de dois círculos, C2 e C3 , cujos raios medem b e c , respectivamente.

III A área de um quadrado cujo lado mede a é igual à área do quadrado cujo lado mede (b + c).


É verdadeiro o que é afirmado apenas em

A
I
B
I e II.
C
II e III.
D
III.
70f7b939-8b
CEDERJ 2019 - Matemática - Álgebra, Equação do 2º Grau e Problemas do 2º Grau

O conjunto de pontos (x, y) do IR2 que satisfazem a equação x2 + y2 + y = 0 é uma

A
parábola que contém os pontos (0,0) e (1/2, - 1/2).
B
elipse com centro em (0,1/2).
C
circunferência de raio igual a 1/2.
D
hipérbole que contém os pontos (1/2, - 1/2) e (-1/2, - 1/2).
710054a4-8b
CEDERJ 2019 - Matemática - Polinômios

Se m e n são números reais tais que o polinômio p(x) = x3 - x2 + mx + n é divisível por x2 + 1, então m - n é igual a

A
0
B
1
C
-2
D
2
7104a9ad-8b
CEDERJ 2019 - Matemática - Seno, Cosseno e Tangente, Trigonometria

Sendo x igual ao cosseno de 2 radianos e y igual ao seno de 2 radianos, conclui-se que

A
x > 0 e y > 0
B
x > 0 e y < 0
C
x < 0 e y > 0
D
x < 0 e y < 0
70ed45f1-8b
CEDERJ 2019 - Matemática - Aritmética e Problemas, Médias

A tabela a seguir fornece um conjunto de dados:



A mediana desse conjunto de dados é igual a

A
6
B
7
C
8
D
9
70f2d5bd-8b
CEDERJ 2019 - Matemática - Probabilidade

Seja S = {n ∈ N tal que 2 ≤ n ≤ 20}. Ao se escolher, aleatoriamente, um elemento de S, a probabilidade de que ele seja primo ou ímpar é

A
0
B
10/19
C
10/18
D
18/19