c76816ae-74
CEDERJ 2021 - Matemática - Sistema de Unidade de Medidas, Aritmética e Problemas, Regra de Três
Para confeccionar 2000 metros de tecido
com largura de 2 m, uma tecelagem consome
400 quilos de fio. Para produzir 2250 metros do
mesmo tecido com largura de 1,40 m, essa
tecelagem precisará de quantos quilos do
mesmo tipo de fio?
Para confeccionar 2000 metros de tecido
com largura de 2 m, uma tecelagem consome
400 quilos de fio. Para produzir 2250 metros do
mesmo tecido com largura de 1,40 m, essa
tecelagem precisará de quantos quilos do
mesmo tipo de fio?
A
280
B
315
C
375
D
450


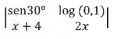 é nulo para o
seguinte valor de
é nulo para o
seguinte valor de