A razão entre homens e mulheres, nessa ordem, em uma turma com 143 pessoas da FGV
equivale à dízima periódica 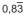 . O número de mulheres dessa turma supera o de homens em
. O número de mulheres dessa turma supera o de homens em
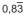 . O número de mulheres dessa turma supera o de homens em
. O número de mulheres dessa turma supera o de homens em 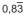 . O número de mulheres dessa turma supera o de homens em
. O número de mulheres dessa turma supera o de homens em 

A tabela indica as vendas de veículos, por categoria, de uma concessionária nos três primeiros
meses de um ano, com a omissão de apenas dois valores, indicados por x e y.

Considerando as três categorias de veículos, a porcentagem de veículos Flex vendidos em
fevereiro foi de
Maria fez um empréstimo bancário a juros compostos de 5% ao mês. Alguns meses após ela quitou a sua dívida, toda de uma só vez, pagando ao banco a quantia de R$ 10 584,00.
Se Maria tivesse pago a sua dívida dois meses antes, ela teria pago ao banco a quantia de
Um pesquisador fez um conjunto de medidas em um laboratório e construiu uma tabela com as frequências relativas (em porcentagem) de cada medida, conforme se vê a seguir:
Valor medido Frequência relativa (%)
1,0 30
1,2 7,5
1,3 45
1,7 12,5
1,8 5
Total = 100
Assim, por exemplo, o valor 1,0 foi obtido em 30% das medidas realizadas. A menor quantidade
possível de vezes que o pesquisador obteve o valor medido maior que 1,5 é
Em uma urna há bolas verdes e bolas amarelas. Se retirarmos uma bola verde da urna, então um quinto das bolas restantes é de bolas verdes. Se retirarmos nove bolas amarelas, em vez de retirar uma bola verde, então um quarto das bolas restantes é de bolas verdes.
O número total de bolas que há inicialmente na urna é
Uma caixa sem tampa é construída a partir de uma chapa retangular de metal, com 8 dm de largura por 10 dm de comprimento, cortando-se, de cada canto da chapa, um quadrado de lado x decímetros e, a seguir, dobrando-se para cima as partes retangulares, conforme sugere a figura a seguir:

O volume, em dm3, da caixa assim obtida é
As notas de cem alunos em uma prova foram colocadas em ordem crescente, originando a sequência de notas n( n1, n2,n3 , ...n100 ).
Sabe-se que
• n1 =0 e n100 =9,6
• podem existir notas iguais;
• n50 ≠ n51
Pode-se afirmar que
Uma fábrica de panelas opera com um custo fixo mensal de R$ 9 800,00 e um custo variável por panela de R$ 45,00. Cada panela é vendida por R$ 65,00. Seja x a quantidade que deve ser produzida e vendida mensalmente para que o lucro mensal seja igual a 20% da receita.
A soma dos algarismos de x é: