Questõesde ENEM sobre Aritmética e Problemas
Um povoado com 100 habitantes está passando por uma situação de seca prolongada e os responsáveis pela administração pública local decidem contratar a construção de um reservatório. Ele deverá ter a forma de um cilindro circular reto, cuja base tenha 5 metros de diâmetro interno, e atender à demanda de água da população por um período de exatamente sete dias consecutivos. No oitavo dia, o reservatório vazio é completamente reabastecido por carros-pipa.
Considere que o consumo médio diário por habitante é de 120 litros de água. Use 3 como aproximação para π.
Nas condições apresentadas, o reservatório deverá ser construído com uma altura interna mínima, em metro, igual a
O sistema de numeração romano ainda é utilizado na indicação de capítulos e volumes de livros, na designação de séculos e, em ordem cronológica, de papas e reis de mesmo nome. São utilizadas sete letras do alfabeto:
Quatro fundamentais: I (vale 1); X (vale 10); C (vale 100) e M (vale 1 000).
Três secundárias: V (vale 5); L (vale 50) e D (vale 500).
As regras para escrever números romanos são:1. Não existe símbolo correspondente ao zero;2. Os símbolos fundamentais podem ser repetidos até três vezes e seus valores são adicionados. Exemplo: XXX = 30;3. Uma letra posta à esquerda de outra de maior valor indica subtração dos respectivos valores. Exemplo: IX = 10 - 1 = 9;4. Uma letra posta à direita de outra de maior valor indica adição dos respectivos valores. Exemplo: XI = 10 + 1 = 11.
Em uma cidade europeia há uma placa indicando o ano de sua fundação: MCDLXIX.
Quantos anos de fundação essa cidade comemorará em 2050?
A relação de Newton-Laplace estabelece que o módulo volumétrico de um fluido é diretamente proporcional ao quadrado da velocidade do som (em metro por segundo) no fluido e à sua densidade (em quilograma por metro cúbico), com uma constante de proporcionalidade adimensional.
Nessa relação, a unidade de medida adequada para o módulo volumétrico é
Uma pessoa comprou uma caneca para tomar sopa, conforme ilustração.

Sabe-se que 1 cm3 = 1 mL e que o topo da caneca é uma circunferência de diâmetro (D) medindo 10 cm, e a base é um círculo de diâmetro (d) medindo 8 cm. Além disso, sabe-se que a altura (h) dessa caneca mede 12 cm (distância entre o centro das circunferências do topo e da base).
Utilize 3 como aproximação para π.
Qual é a capacidade volumétrica, em mililitro, dessa caneca?

Para realizar um voo entre duas cidades que distam 2 000 km uma da outra, uma companhia aérea utilizava um modelo de aeronave A, capaz de transportar até 200 passageiros. Quando uma dessas aeronaves está lotada de passageiros, o consumo de combustível é de 0,02 litro por quilômetro e por passageiro. Essa companhia resolveu trocar o modelo de aeronave A pelo modelo de aeronave B, que é capaz de transportar 10% de passageiros a mais do que o modelo A, mas consumindo 10% menos combustível por quilômetro e por passageiro.
A quantidade de combustível consumida pelo modelo de aeronave B, em relação à do modelo de aeronave A, em um voo lotado entre as duas cidades, é
Em um estudo realizado pelo IBGE em quatro estados e no Distrito Federal, com mais de 5 mil pessoas com 10 anos ou mais, observou-se que a leitura ocupa, em média, apenas seis minutos do dia de cada pessoa. Na faixa de idade de 10 a 24 anos, a média diária é de três minutos. No entanto, no grupo de idades entre 24 e 60 anos, o tempo médio diário dedicado à leitura é de 5 minutos. Entre os mais velhos, com 60 anos ou mais, a média é de 12 minutos.
A quantidade de pessoas entrevistadas de cada faixa de idade seguiu a distribuição percentual descrita no quadro.

Disponível em: www.oglobo.globo.com. Acesso em: 16 ago. 2013 (adaptado).
Os valores de x e y do quadro são, respectivamente, iguais a

Um segmento de reta está dividido em duas partes na proporção áurea quando o todo está para uma das partes na mesma razão em que essa parte está para a outra. Essa constante de proporcionalidade é comumente representada pela letra grega φ, e seu valor é dado pela solução positiva da equação φ2 = φ + 1.
Assim como a potência φ2, as potências superiores de φ podem ser expressas da forma aφ + b, em que a e b são inteiros positivos, como apresentado no quadro.

A potência φ7, escrita na forma aφ + b {a e b são inteiros positivos), é

Um atleta produz sua própria refeição com custo fixo de R$ 10,00. Ela é composta por 400 g de frango, 600 g de batata-doce e uma hortaliça. Atualmente, os preços dos produtos para essa refeição são:

Em relação a esses preços, haverá um aumento de 50% no preço do quilograma de batata-doce, e os outros preços não serão alterados. O atleta deseja manter o custo da refeição, a quantidade de batata-doce e a hortaliça.
Portanto, terá que reduzir a quantidade de frango. Qual deve ser a redução percentual da quantidade de frango para que o atleta alcance seu objetivo?

Um nutricionista verificou, na dieta diária do seu cliente, a falta de 800 mg do mineral A, de 1 000 mg do mineral B e de 1 200 mg do mineral C. Por isso, recomendou a compra de suplementos alimentares que forneçam os minerais faltantes e informou que não haveria problema se consumisse mais desses minerais do que o recomendado.
O cliente encontrou cinco suplementos, vendidos em saches unitários, cujos preços e as quantidades dos minerais estão apresentados a seguir:
• Suplemento I: contém 50 mg do mineral A, 100 mg do mineral B e 200 mg do mineral C e custa R$ 2,00;• Suplemento II: contém 800 mg do mineral A, 250 mg do mineral B e 200 mg do mineral C e custa R$ 3,00;• Suplemento III: contém 250 mg do mineral A, 1 000 mg do mineral B e 300 mg do mineral C e custa R$ 5,00;• Suplemento IV: contém 600 mg do mineral A, 500 mg do mineral B e 1 000 mg do mineral C e custa R$ 6,00;• Suplemento V: contém 400 mg do mineral A, 800 mg do mineral B e 1 200 mg do mineral C e custa R$ 8,00.
O cliente decidiu comprar sachês de um único suplemento no qual gastasse menos dinheiro e ainda suprisse a falta de minerais indicada pelo nutricionista, mesmo que consumisse alguns deles além de sua necessidade.
Nessas condições, o cliente deverá comprar sachês do suplemento
O dono de uma loja pretende usar cartões imantados para a divulgação de sua loja.
A empresa que fornecerá o serviço lhe informa que o custo de fabricação do cartão é de
R$ 0,01 por centímetro quadrado e que disponibiliza modelos tendo como faces úteis
para impressão:
- um triângulo equilátero de lado 12 cm;
- um quadrado de lado 8 cm;
- um retângulo de lados 11 cm e 8 cm;
- um hexágono regular de lado 6 cm;
- um círculo de diâmetro 10 cm.
O dono da loja está disposto a pagar, no máximo, R$ 0,80 por cartão. Ele escolherá,
dentro desse limite de preço, o modelo que tiver maior área de impressão.
Use 3 como aproximação para π e use 1,7 como aproximação para √3.
Nessas condições, o modelo que deverá ser escolhido tem como face útil para impressão
um
- um triângulo equilátero de lado 12 cm;
- um quadrado de lado 8 cm;
- um retângulo de lados 11 cm e 8 cm;
- um hexágono regular de lado 6 cm;
- um círculo de diâmetro 10 cm.
O dono da loja está disposto a pagar, no máximo, R$ 0,80 por cartão. Ele escolherá, dentro desse limite de preço, o modelo que tiver maior área de impressão.
Use 3 como aproximação para π e use 1,7 como aproximação para √3.
Nessas condições, o modelo que deverá ser escolhido tem como face útil para impressão um
Uma pessoa comprou uma caneca para tomar sopa, conforme ilustração.

Sabe-se que 1 cm3 = 1 mL e que o topo da caneca é uma circunferência de
diâmetro (D) medindo 10 cm, e a base é um círculo de diâmetro (d) medindo 8 cm. Além
disso, sabe-se que a altura (h) dessa caneca mede 12 cm (distância entre o centro das
circunferências do topo e da base).
Utilize 3 como aproximação para π.
Qual é a capacidade volumétrica, em mililitro, dessa caneca?
Uma pessoa comprou uma caneca para tomar sopa, conforme ilustração.
Sabe-se que 1 cm3 = 1 mL e que o topo da caneca é uma circunferência de diâmetro (D) medindo 10 cm, e a base é um círculo de diâmetro (d) medindo 8 cm. Além disso, sabe-se que a altura (h) dessa caneca mede 12 cm (distância entre o centro das circunferências do topo e da base).
Utilize 3 como aproximação para π.
Qual é a capacidade volumétrica, em mililitro, dessa caneca?
Um atleta produz sua própria refeição com custo fixo de R$ 10,00. Ela é composta
por 400 g de frango, 600 g de batata-doce e uma hortaliça. Atualmente, os preços dos
produtos para essa refeição são:

Em relação a esses preços, haverá um aumento de 50% no preço do quilograma de
batata-doce, e os outros preços não serão alterados. O atleta deseja manter o custo da
refeição, a quantidade de batata-doce e a hortaliça. Portanto, terá que reduzir a
quantidade de frango.
Qual deve ser a redução percentual da quantidade de frango para que o atleta alcance
seu objetivo?

Para realizar um voo entre duas cidades que distam 2 000 km uma da outra, uma
companhia aérea utilizava um modelo de aeronave A, capaz de transportar até
200 passageiros. Quando uma dessas aeronaves está lotada de passageiros, o consumo
de combustível é de 0,02 litro por quilômetro e por passageiro. Essa companhia resolveu
trocar o modelo de aeronave A pelo modelo de aeronave B, que é capaz de transportar
10% de passageiros a mais do que o modelo A, mas consumindo 10% menos
combustível por quilômetro e por passageiro.
A quantidade de combustível consumida pelo modelo de aeronave B, em relação à do
modelo de aeronave A, em um voo lotado entre as duas cidades, é
O sistema de numeração romano ainda é utilizado na indicação de capítulos e
volumes de livros, na designação de séculos e, em ordem cronológica, de papas e reis de
mesmo nome. São utilizadas sete letras do alfabeto:
Quatro fundamentais: I (vale 1); X (vale 10); C (vale 100) e M (vale 1 000).
Três secundárias: V (vale 5); L (vale 50) e D (vale 500).
As regras para escrever números romanos são:
1. Não existe símbolo correspondente ao zero;
2. Os símbolos fundamentais podem ser repetidos até três vezes e seus valores são
adicionados. Exemplo: XXX = 30;
3. Uma letra posta à esquerda de outra de maior valor indica subtração dos respectivos
valores. Exemplo: IX = 10 – 1 = 9;
4. Uma letra posta à direita de outra de maior valor indica adição dos respectivos valores.
Exemplo: XI = 10 + 1 = 11.
Em uma cidade europeia há uma placa indicando o ano de sua fundação: MCDLXIX.
Quantos anos de fundação essa cidade comemorará em 2050?
O instrumento de percussão conhecido como triângulo é composto por uma barra
fina de aço, dobrada em um formato que se assemelha a um triângulo, com uma abertura
e uma haste, conforme ilustra a Figura 1.
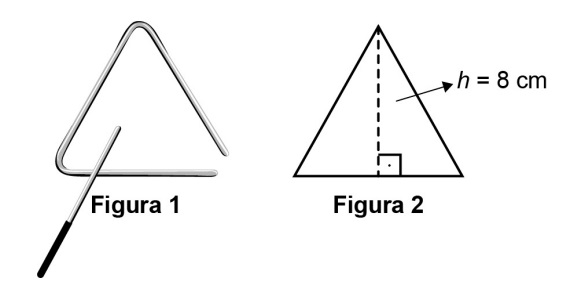

Uma empresa de brindes promocionais contrata uma fundição para a produção de
miniaturas de instrumentos desse tipo. A fundição produz, inicialmente, peças com o
formato de um triângulo equilátero de altura h, conforme ilustra a Figura 2. Após esse
processo, cada peça é aquecida, deformando os cantos, e cortada em um dos vértices,
dando origem à miniatura. Assuma que não ocorram perdas de material no processo de
produção, de forma que o comprimento da barra utilizada seja igual ao perímetro do
triângulo equilátero representado na Figura 2.
Considere 1,7 como valor aproximado para √3.
Nessas condições, o valor que mais se aproxima da medida do comprimento da barra, em
centímetro, é


Uma unidade de medida comum usada para expressar áreas de terrenos de grandes
dimensões é o hectare, que equivale a 10 000 m2 . Um fazendeiro decide fazer um
loteamento utilizando 3 hectares de sua fazenda, dos quais 0,9 hectare será usado para a
construção de ruas e calçadas e o restante será dividido em terrenos com área de 300 m2 cada um. Os 20 primeiros terrenos vendidos terão preços promocionais de R$ 20 000,00
cada, e os demais, R$ 30 000,00 cada.
Nas condições estabelecidas, o valor total, em real, obtido pelo fazendeiro com a venda
de todos os terrenos será igual a
Um automóvel apresenta um desempenho médio de 16 km/L. Um engenheiro
desenvolveu um novo motor a combustão que economiza, em relação ao consumo do
motor anterior, 0,1 L de combustível a cada 20 km percorridos.
O valor do desempenho médio do automóvel com o novo motor, em quilômetro por litro,
expresso com uma casa decimal, é
Uma pessoa pretende viajar por uma companhia aérea que despacha gratuitamente
uma mala com até 10 kg.
Em duas viagens que realizou, essa pessoa utilizou a mesma mala e conseguiu
10 kg com as seguintes combinações de itens:

Para ter certeza de que sua bagagem terá massa de 10 kg, ela decide levar essa
mala com duas calças, um sapato e o máximo de camisetas, admitindo que itens do
mesmo tipo têm a mesma massa.
Qual a quantidade máxima de camisetas que essa pessoa poderá levar?

Um nutricionista verificou, na dieta diária do seu cliente, a falta de 800 mg do
mineral A, de 1 000 mg do mineral B e de 1 200 mg do mineral C. Por isso, recomendou a
compra de suplementos alimentares que forneçam os minerais faltantes e informou que
não haveria problema se consumisse mais desses minerais do que o recomendado.
O cliente encontrou cinco suplementos, vendidos em sachês unitários, cujos preços e
as quantidades dos minerais estão apresentados a seguir:
-
Suplemento I: contém 50 mg do mineral A, 100 mg do mineral B e 200 mg do
mineral C e custa R$ 2,00;
- Suplemento II: contém 800 mg do mineral A, 250 mg do mineral B e 200 mg do
mineral C e custa R$ 3,00;
- Suplemento III: contém 250 mg do mineral A, 1 000 mg do mineral B e 300 mg do
mineral C e custa R$ 5,00;
- Suplemento IV: contém 600 mg do mineral A, 500 mg do mineral B e 1 000 mg do
mineral C e custa R$ 6,00;
- Suplemento V: contém 400 mg do mineral A, 800 mg do mineral B e 1 200 mg do
mineral C e custa R$ 8,00.
O cliente decidiu comprar sachês de um único suplemento no qual gastasse menos
dinheiro e ainda suprisse a falta de minerais indicada pelo nutricionista, mesmo que
consumisse alguns deles além de sua necessidade.
Nessas condições, o cliente deverá comprar sachês do suplemento
- Suplemento I: contém 50 mg do mineral A, 100 mg do mineral B e 200 mg do mineral C e custa R$ 2,00;
- Suplemento II: contém 800 mg do mineral A, 250 mg do mineral B e 200 mg do mineral C e custa R$ 3,00;
- Suplemento III: contém 250 mg do mineral A, 1 000 mg do mineral B e 300 mg do mineral C e custa R$ 5,00;
- Suplemento IV: contém 600 mg do mineral A, 500 mg do mineral B e 1 000 mg do mineral C e custa R$ 6,00;
- Suplemento V: contém 400 mg do mineral A, 800 mg do mineral B e 1 200 mg do mineral C e custa R$ 8,00.
O cliente decidiu comprar sachês de um único suplemento no qual gastasse menos
dinheiro e ainda suprisse a falta de minerais indicada pelo nutricionista, mesmo que
consumisse alguns deles além de sua necessidade.
Nessas condições, o cliente deverá comprar sachês do suplemento