Questõessobre Ângulos - Lei Angular de Thales
As Artes Marciais Mistas, tradução do inglês: MMA -
mixed martial arts, são realizadas num octógono regular.
De acordo com a figura, em certo momento os dois
lutadores estão respectivamente nas posições G e F, e
o juiz está na posição I. O triângulo IGH é equilátero e
GIF é o ângulo formado pelas semirretas com origem
na posição do juiz, respectivamente passando pelas
posições de cada um dos lutadores.

A medida do ângulo GIF é
As Artes Marciais Mistas, tradução do inglês: MMA - mixed martial arts, são realizadas num octógono regular. De acordo com a figura, em certo momento os dois lutadores estão respectivamente nas posições G e F, e o juiz está na posição I. O triângulo IGH é equilátero e GIF é o ângulo formado pelas semirretas com origem na posição do juiz, respectivamente passando pelas posições de cada um dos lutadores.

A medida do ângulo GIF é
Isometria é uma transformação geométrica que, aplicada a uma figura, mantém as distâncias entre pontos. Duas das
transformações isométricas são a reflexão e a rotação. A reflexão ocorre por meio de uma reta chamada eixo. Esse eixo
funciona como um espelho, a imagem refletida é o resultado da transformação. A rotação é o “giro” de uma figura ao redor de
um ponto chamado centro de rotação. A figura sofreu cinco transformações isométricas, nessa ordem:

1ª) Reflexão no eixo x;
2ª) Rotação de 90 graus no sentido anti-horário, com centro de rotação no ponto A;
3ª) Reflexão no eixo y;
4ª) Rotação de 45 graus no sentido horário, com centro de rotação no ponto A;
5ª) Reflexão no eixo x.
Disponível em: www.pucsp.br. Acesso em: 2 ago. 2012.
Qual a posição final da figura?
Isometria é uma transformação geométrica que, aplicada a uma figura, mantém as distâncias entre pontos. Duas das transformações isométricas são a reflexão e a rotação. A reflexão ocorre por meio de uma reta chamada eixo. Esse eixo funciona como um espelho, a imagem refletida é o resultado da transformação. A rotação é o “giro” de uma figura ao redor de um ponto chamado centro de rotação. A figura sofreu cinco transformações isométricas, nessa ordem:

1ª) Reflexão no eixo x;
2ª) Rotação de 90 graus no sentido anti-horário, com centro de rotação no ponto A;
3ª) Reflexão no eixo y;
4ª) Rotação de 45 graus no sentido horário, com centro de rotação no ponto A;
5ª) Reflexão no eixo x.
Disponível em: www.pucsp.br. Acesso em: 2 ago. 2012.
Qual a posição final da figura?





Se dois círculos cujas medidas dos raios são
respectivamente u e v com u < v são tangentes
exteriormente no ponto P e se estes círculos também
tangenciam os lados de um ângulo com vértice no
ponto M, então, o comprimento do segmento MP é




No triângulo ABC exibido na figura a seguir, AD é a
bissetriz do ângulo interno em A, e  O ângulo
interno em A é igual a
O ângulo
interno em A é igual a

No triângulo ABC exibido na figura a seguir, AD é a
bissetriz do ângulo interno em A, e  O ângulo
interno em A é igual a
O ângulo
interno em A é igual a

A rosa dos ventos é uma figura que representa oito
sentidos, que dividem o círculo em partes iguais.

Uma câmera de vigilância está fixada no teto de um
shopping e sua lente pode ser direcionada remotamente,
através de um controlador, para qualquer sentido. A lente
da câmera está apontada inicialmente no sentido Oeste
e o seu controlador efetua três mudanças consecutivas,
a saber:
• 1ª mudança: 135° no sentido anti-horário;
• 2ª mudança: 60° no sentido horário;
• 3ª mudança: 45° no sentido anti-horário.
Após a 3ª mudança, ele é orientado a reposicionar
a câmera, com a menor amplitude possível, no sentido
Noroeste (NO) devido a um movimento suspeito de
um cliente.
Qual mudança de sentido o controlador deve efetuar para
reposicionar a câmera?
A rosa dos ventos é uma figura que representa oito sentidos, que dividem o círculo em partes iguais.

Uma câmera de vigilância está fixada no teto de um shopping e sua lente pode ser direcionada remotamente, através de um controlador, para qualquer sentido. A lente da câmera está apontada inicialmente no sentido Oeste e o seu controlador efetua três mudanças consecutivas, a saber:
• 1ª mudança: 135° no sentido anti-horário;
• 2ª mudança: 60° no sentido horário;
• 3ª mudança: 45° no sentido anti-horário.
Após a 3ª mudança, ele é orientado a reposicionar a câmera, com a menor amplitude possível, no sentido Noroeste (NO) devido a um movimento suspeito de um cliente.
Qual mudança de sentido o controlador deve efetuar para
reposicionar a câmera?
Se
a
e
b
são ângulos agudos e
complementares, o valor da expressão
sen²(a+b) – cos ²(a+b) é
No gráfico, representado a seguir, uma das retas esboçadas tem inclinação
igual a – 3 e a outra reta, inclinação igual a 1/2 . Sabendo-se disso, a área
(em unidade de área) da região hachurada é


O símbolo internacional de acesso, mostrado na figura,
anuncia local acessível para o portador de necessidades
especiais. Na concepção desse símbolo, foram empregados
elementos gráficos geométricos elementares.

Os elementos geométricos que constituem os contornos
das partes claras da figura são
O símbolo internacional de acesso, mostrado na figura, anuncia local acessível para o portador de necessidades especiais. Na concepção desse símbolo, foram empregados elementos gráficos geométricos elementares.

Os elementos geométricos que constituem os contornos
das partes claras da figura são
Em uma sala de aula, três alunos resolveram fazer
uma brincadeira de medição. Cada um escolheu um
objeto próprio para medir o comprimento da lousa. O
primeiro foi até a lousa e, usando o comprimento de
um livro, verificou que era possível enfileirar 13 deles
e ainda sobrava um pequeno espaço igual à metade
do comprimento do livro. O segundo pegou seu lápis
e começou a medir a lousa. No final, percebeu que
esse comprimento era igual a 20 lápis. O terceiro,
para economizar tempo, pegou uma régua graduada e
mediu o comprimento do livro que o colega havia usado,
obtendo 28 cm.
Com base nessas informações, qual é a medida mais
aproximada do comprimento do lápis?
Em uma sala de aula, três alunos resolveram fazer uma brincadeira de medição. Cada um escolheu um objeto próprio para medir o comprimento da lousa. O primeiro foi até a lousa e, usando o comprimento de um livro, verificou que era possível enfileirar 13 deles e ainda sobrava um pequeno espaço igual à metade do comprimento do livro. O segundo pegou seu lápis e começou a medir a lousa. No final, percebeu que esse comprimento era igual a 20 lápis. O terceiro, para economizar tempo, pegou uma régua graduada e mediu o comprimento do livro que o colega havia usado, obtendo 28 cm.
Com base nessas informações, qual é a medida mais aproximada do comprimento do lápis?
No labirinto em um parque de diversões, representado
pela malha quadriculada, encontram-se sete crianças:
Ana, Carol, Samanta, Denise, Roberta, Eliana e Larissa,
representadas por pontos, identificados pela letra inicial
do nome de cada uma delas. A malha é formada por
quadrados, cujos lados medem 1 cm.

Considere que cada criança pode se deslocar apenas na
direção vertical ou horizontal dentro do labirinto. Desse
modo, Ana encontra-se equidistante de Samanta e de
No labirinto em um parque de diversões, representado pela malha quadriculada, encontram-se sete crianças: Ana, Carol, Samanta, Denise, Roberta, Eliana e Larissa, representadas por pontos, identificados pela letra inicial do nome de cada uma delas. A malha é formada por quadrados, cujos lados medem 1 cm.

Considere que cada criança pode se deslocar apenas na
direção vertical ou horizontal dentro do labirinto. Desse
modo, Ana encontra-se equidistante de Samanta e de
Um polígono convexo de 6 lados tem as medidas de seus ângulos internos formando uma progressão aritmética de razão igual a 6º. Logo, podemos afirmar que o seu menor ângulo mede:
Prolongando-se os lados de um octógono convexo ABCDEFGH,
obtém-se um polígono estrelado, conforme a figura.

A soma α1 +... + αB vale
Prolongando-se os lados de um octógono convexo ABCDEFGH, obtém-se um polígono estrelado, conforme a figura.

A soma α1 +... + αB vale
A imagem apresentada na figura é uma cópia em preto
e branco da tela quadrada intitulada O peixe, de Marcos
Pinto, que foi colocada em uma parede para exposição e
fixada nos pontos A e B.
Por um problema na fixação de um dos pontos, a tela
se desprendeu, girando rente à parede. Após o giro, ela
ficou posicionada como ilustrado na figura, formando um
ângulo de 45° com a linha do horizonte.

Para recolocar a tela na sua posição original, deve-se
girá-la, rente à parede, no menor ângulo possível inferior
a 360°.
A forma de recolocar a tela na posição original, obedecendo
ao que foi estabelecido, é girando-a em um ângulo de
A imagem apresentada na figura é uma cópia em preto e branco da tela quadrada intitulada O peixe, de Marcos Pinto, que foi colocada em uma parede para exposição e fixada nos pontos A e B.
Por um problema na fixação de um dos pontos, a tela se desprendeu, girando rente à parede. Após o giro, ela ficou posicionada como ilustrado na figura, formando um ângulo de 45° com a linha do horizonte.

Para recolocar a tela na sua posição original, deve-se girá-la, rente à parede, no menor ângulo possível inferior a 360°.
A forma de recolocar a tela na posição original, obedecendo
ao que foi estabelecido, é girando-a em um ângulo de
A matriz abaixo apresenta a distribuição das matrículas,
por níveis, nas escolas de Porto Alegre. Se esses dados forem organizados em um gráfico
de setores, o ângulo central correspondente ao nível
Fundamental será de, aproximadamente,
Se esses dados forem organizados em um gráfico
de setores, o ângulo central correspondente ao nível
Fundamental será de, aproximadamente,



Uma mesa de passar roupa possui pernas articuladas 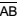 e
e 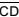 , conforme indica a figura. Sabe-se que AB = CD = 1 m, e que M é ponto médio dos segmentos coplanares
, conforme indica a figura. Sabe-se que AB = CD = 1 m, e que M é ponto médio dos segmentos coplanares 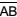 e
e 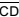 . Quando a mesa está armada, o tampo fica paralelo ao plano do chão e a medida do ângulo
. Quando a mesa está armada, o tampo fica paralelo ao plano do chão e a medida do ângulo 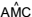 é 60º.
é 60º.

Considerando-se desprezíveis as medidas dos pés e da espessura do tampo e adotando √3 = 1,7, a altura do tampo dessa mesa armada em relação ao plano do chão, em centímetros, está entre
Uma mesa de passar roupa possui pernas articuladas 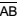 e
e 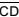 , conforme indica a figura. Sabe-se que AB = CD = 1 m, e que M é ponto médio dos segmentos coplanares
, conforme indica a figura. Sabe-se que AB = CD = 1 m, e que M é ponto médio dos segmentos coplanares 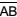 e
e 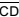 . Quando a mesa está armada, o tampo fica paralelo ao plano do chão e a medida do ângulo
. Quando a mesa está armada, o tampo fica paralelo ao plano do chão e a medida do ângulo 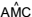 é 60º.
é 60º.

Considerando-se desprezíveis as medidas dos pés e da espessura do tampo e adotando √3 = 1,7, a altura do tampo dessa mesa armada em relação ao plano do chão, em centímetros, está entre
Na figura a seguir, o quadrilátero ABCD é um paralelogramo, em que os
segmentos orientados  e
e  representam duas forças, sendo med(
representam duas forças, sendo med(  ) = 80,
med(
) = 80,
med(  )= 100 e med(
)= 100 e med(  ) = 120°.
) = 120°.

Assinale a alternativa que contém a afirmação correta sobre a med(  ) do
segmento
) do
segmento  , e sobre a medida q do ângulo
, e sobre a medida q do ângulo  .
.
 e
e  representam duas forças, sendo med(
representam duas forças, sendo med(  ) = 80,
med(
) = 80,
med(  )= 100 e med(
)= 100 e med(  ) = 120°.
) = 120°. 
Assinale a alternativa que contém a afirmação correta sobre a med(
 ) do
segmento
) do
segmento  , e sobre a medida q do ângulo
, e sobre a medida q do ângulo  .
.  = 50 e q = 30°
= 50 e q = 30°
 = 130 e q = 30°
= 130 e q = 30°
 = 130 e q > 30°
= 130 e q > 30° = 50 e q < 30°
= 50 e q < 30° = 85 e q = 30°
= 85 e q = 30°
Na figura seguinte, as retas r e s são paralelas entre si, e
perpendiculares à reta t. Sabe-se, ainda, que AB = 6 cm,
CD = 3 cm,  é perpendicular a
é perpendicular a  , e a medida do ângulo
entre
, e a medida do ângulo
entre  e a reta s é 30°.
e a reta s é 30°.

Nas condições descritas, a medida de  , em cm, é igual a
, em cm, é igual a
 é perpendicular a
é perpendicular a  , e a medida do ângulo
entre
, e a medida do ângulo
entre  e a reta s é 30°.
e a reta s é 30°.
Nas condições descritas, a medida de
 , em cm, é igual a
, em cm, é igual a