Considerando-se a matriz M =  e sua transposta Mt, pode-se afirmar que a matriz soma (M + Mt) é igual a
e sua transposta Mt, pode-se afirmar que a matriz soma (M + Mt) é igual a
Considerando-se a matriz M =  e sua transposta Mt, pode-se afirmar que a matriz soma (M + Mt) é igual a
e sua transposta Mt, pode-se afirmar que a matriz soma (M + Mt) é igual a




Considerando-se a matriz M =  e sua transposta Mt, pode-se afirmar que a matriz soma (M + Mt) é igual a
e sua transposta Mt, pode-se afirmar que a matriz soma (M + Mt) é igual a






Considerando-se as matrizes L = M =
M = e N =
e N =  após análise das proposições a seguir, assinale V para as verdadeiras e F, para as falsas.
após análise das proposições a seguir, assinale V para as verdadeiras e F, para as falsas.
( ) L−1
= 1/4 
( ) 3M + Nt
= 
( ) O determinante de L é 6.
( ) O sistema S = M tem infinitas soluções.
tem infinitas soluções.
A alternativa que indica a sequência correta, de cima para baixo, é a
Se a matriz 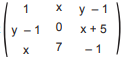 é simétrica, então o valor de xy é
é simétrica, então o valor de xy é
Se M é uma matriz tal que M² =  , então det (M−1) é igual a
, então det (M−1) é igual a
Determine a solução da inequação  dentre as apontadas nas alternativas a seguir.
dentre as apontadas nas alternativas a seguir.
Sobre o sistema linear , a, b reais, pode-se afirmar que é
, a, b reais, pode-se afirmar que é
Considere uma matriz C, tal que C = A. B.
Se  e
e  então o determinante de C é
então o determinante de C é
Laerte, nascido em Guarapuava, mudou-se para Irati, ainda no Paraná, e para manter secreta sua correspondência com Carol, concebeu um código, como descrito a seguir:
1o Associou números às letras do alfabeto:

2o Escolheu a matriz código 
3o Associou o número 0 ao espaço entre palavras.
4o A frase foi transformada em uma matriz que somada à matriz código C resulta na matriz mensagem M, assim A + C = M.
Dessa forma, a palavra DIA corresponde à matriz  que, somada à matriz código,
resultará na matriz mensagem
que, somada à matriz código,
resultará na matriz mensagem 
Usando o processo criado por Laerte, a mensagem  decodificada corresponde a
decodificada corresponde a
30m.
Considerando-se as matrizes  e MN = P, pode-se afirmar que
o valor do determinante de M é
e MN = P, pode-se afirmar que
o valor do determinante de M é
Dado o sistema , em que a e b são números reais, assinale a alternativa correta.
, em que a e b são números reais, assinale a alternativa correta.
Sejam as matrizes A, B e C dadas por

Assinale a alternativa correta.
