b378ac81-b6
UFVJM-MG 2016 - Matemática - Matrizes, Álgebra Linear
Dada a matriz 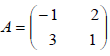 e sabendo que a matriz B é igual à transposta de A, ou seja, B = A t o determinante da matriz X dada por X = AB, é
e sabendo que a matriz B é igual à transposta de A, ou seja, B = A t o determinante da matriz X dada por X = AB, é
Dada a matriz 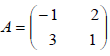 e sabendo que a matriz B é igual à transposta de A, ou seja, B = A t o determinante da matriz X dada por X = AB, é
e sabendo que a matriz B é igual à transposta de A, ou seja, B = A t o determinante da matriz X dada por X = AB, é
A
49
B
50
C
51
D
52










