Questõesde UECE sobre Álgebra Linear

InícioTodas as questões
1
1
1
Foram encontradas 34 questões
09528c28-75
UECE 2021 - Matemática - Matrizes, Álgebra Linear

Considere a matriz , onde x e y são números reais. Se M2 = M.M, então, o determinante de M2 é igual a

A
(x2 + y2 )2 .
B
(x2 - y2 )2 .
C
x4 - y4 .
D
x4 + y4 .
ffc14736-58
UECE 2021 - Matemática - Matrizes, Álgebra Linear

Considerando-se as matrizes e Z = (2X).Y, é correto afirmar que o determinante da matriz Z é igual a 

A
12.
B
16.
C
4.
D
0.
32c10616-0b
UECE 2021 - Matemática - Matrizes, Álgebra Linear

Se M é a matriz M = e det(M) é o determinante de M, então, para um número inteiro k, todas as soluções x da equação det(M) = 0 são da forma

A
π/2+ 2k π.
B
π + k π.
C
π + 2k π.
D
π/2+ k π.
afd82bc4-0a
UECE 2021 - Matemática - Matrizes, Álgebra Linear

Considere as matrizes reais M = e N = Se o determinante de M é igual a 2 e o determinante de N é igual a 1, então, o produto a.b pode ser igual a

A
–1 ou 2.
B
1 ou –2.
C
–1 ou –2.
D
1 ou 2.
16492ad7-02
UECE 2018 - Matemática - Matrizes, Álgebra Linear

Sejam d(x) e D(x) respectivamente os determinantes das matrizes m = e M = onde y = senx, com x pertencendo ao intervalo fechado [0,2 π]. Se n é o número de valores de x tais que d(x) + D(x) = 0, então, é correto afirmar que n é igual a

A
5.
B
4.
C
3.
D
2.
163258d7-02
UECE 2018 - Matemática - Álgebra Linear, Sistemas Lineares

Se o sistema de equações   Onde a = sen α e b = cos α, admite uma única solução, então, pode-se afirmar corretamente que

A
2 α ≠ k π, onde k é um número inteiro.
B
α = k π, onde k é um número inteiro.
C
α = (2k + 1) π, onde k é um número inteiro.
D
2 α ≠ 1 + k π, onde k é um número inteiro.
5b94b5df-ff
UECE 2019 - Matemática - Matrizes, Álgebra Linear

Na matriz  os números reais x1, x2 ,x3 e x4 formam, nessa ordem, uma progressão geométrica crescente cujo primeiro termo é maior do que zero. Se q é a razão dessa progressão, é correto afirmar que o determinante da matriz M (detM) satisfaz a dupla desigualdade

A
–q < detM < q.
B
0 < detM < q.
C
0 < detM < x1 .q.
D
x1 < detM < x1 . q.
ae35383c-fd
UECE 2019 - Matemática - Álgebra Linear, Sistemas Lineares

Os valores de k para os quais x = y = z = 0 seja a única solução do sistema 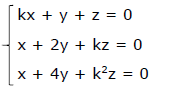NÃO pertencem ao conjunto

A
{1, 2, –1/2}.
B
{–1, –2, –1/6}.
C
{–1, 3, –1/5}.
D
{–1, –2, –1/4}.
ae1e1133-fd
UECE 2019 - Matemática - Matrizes, Álgebra Linear

Considere as matrizes M = e N = 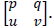Se M.N = N.M, é correto afirmar que o determinante da matriz N é igual a

A
2p2 - 3q2 / 3
B
3p2 - 2q2 / 3
C
3p2 - 2q2/2.
D
2p2-3q2/2.
828fbb66-b8
UECE 2013 - Matemática - Matrizes, Álgebra Linear

Uma matriz quadrada P = (aij) é simétrica quando aij = aji. Por exemplo, a matriz é simétrica.

Se a matriz é simétrica

pode-se afirmar corretamente que o determinante de M é igual a

A
-1.
B
-2.
C
1.
D
2.
82611e7a-b8
UECE 2013 - Matemática - Progressão Geométrica - PG, Matrizes, Álgebra Linear, Progressões

Se os números reais x, y, z, m, n, p, u, v, w formam, nesta ordem, uma progressão geométrica de razão q, então o valor do determinante da matriz é

A
1.
B
0.
C
xnw.
D
q³ .
cdb51c3b-b8
UECE 2019 - Matemática - Matrizes, Álgebra Linear

Considere a matriz , em que x e y são números reais. Se det(M) representa o determinante da matriz M, então, em um plano com o sistema de coordenadas cartesiano usual, a equação det(M) = – 4 expressa a equação de uma reta. A distância dessa reta à origem do sistema de coordenadas é igual a

u.c. ≡ unidade de comprimento

A
√2/ 2 u.c.
B
√2/ 3 u.c.
C
√3/ 2 u.c.
D
√3 u.c.
09c330d7-bb
UECE 2014 - Matemática - Matrizes, Álgebra Linear

Desenvolvendo o determinante abaixo, obtém-se uma equação do segundo grau.



A raiz positiva desta equação é

A
10.
B
15.
C
20.
D
25.
6b8668f1-b9
UECE 2014 - Matemática - Matrizes, Álgebra Linear

Se x é um ângulo tal que cos x = 1/4 , então o valor do determinante  é

A

1.

B

0.

C

1/2.

D
- 1/2.
de367016-b9
UECE 2016 - Matemática - Matrizes, Álgebra Linear

Se V é uma matriz quadrada e n é um número natural maior do que um, define-se Vn = V.Vn-1 .

Com essa definição, para a matriz V = pode-se afirmar corretamente que o valor do determinante da matriz Y = V + V2 + V3 + ... V2016 é igual a

A
2 x 2016.
B
2 x 2017.
C
2016 x 2016.
D
2016 x 2017.
9d97f917-b7
UECE 2012 - Matemática - Álgebra Linear - Equações Lineares, Espaço Vetorial e Transformações Lineares e Matrizes, Pontos e Retas, Geometria Analítica, Álgebra Linear

Sejam r e s retas paralelas cuja distância entre elas é 3m e MN um segmento unitário sobre a reta s. Se X é um ponto em r tal que a medida do segmento MX é 6m e se P é a projeção ortogonal de N sobre MX ou seu prolongamento, então a medida do segmento NP é

A
1,20m.
B
0,50m.
C
1,00m.
D
0,80m.
078ae6d4-b6
UECE 2009 - Matemática - Matrizes, Álgebra Linear

Considere as matrizes 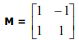e 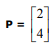. Se a matriz 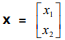é solução da equação matricial M.X = P então o valor de é:

A
4
B
6
C
8
D
10
d7a5a3a3-b8
UECE 2014 - Matemática - Álgebra Linear, Sistemas Lineares

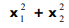Em relação ao sistema pode-se afirmar corretamente que

A
o sistema admite solução não nula apenas quando m = -1.
B
para qualquer valor de m, a solução nula (x = 0, y = 0, z = 0) é a única solução do sistema.
C
o sistema admite solução não nula quando m = 2 ou m = -2.
D
não temos dados suficientes para concluir que o sistema tem solução não nula.
d7991b3c-b8
UECE 2014 - Matemática - Álgebra Linear, Sistemas Lineares

A interseção das curvas representadas no plano, com o sistema cartesiano ortogonal usual,pelas equações x2 + y2 = 1 e │x│+│y│ = √2 é um conjunto

A
vazio.
B
unitário (um ponto).
C
com dois elementos (dois pontos).
D
com quatro elementos (quatro pontos).
a3b28325-b8
UECE 2015 - Matemática - Álgebra Linear, Sistemas Lineares

Considere a solução (x,y) do sistema

sen(x + y) = √3/2

tg(x + y) = √3/3


onde os valores x e y, expressos em radianos, são os menores valores positivos possíveis. Nestas condições a soma x2 + y2 é igual a

A
5π2/72.
B
3π2/16.
C
4π2/15.
D
2π2/5.