Quatro ônibus (representados por 1, 2, 3 e 4) levaram torcedores de um time de futebol para assistir a um jogo em outra cidade. Cada um deles tinha capacidade para 46 passageiros. Durante uma parada, todos os torcedores saíram dos ônibus, mas quando retornaram, vários torcedores não entraram no mesmo ônibus de onde tinham saído. Além disso, o ônibus 4 apresentou defeito, não pôde continuar a viagem e seus ocupantes tiveram que se acomodar nos três ônibus restantes.
Na matriz A, abaixo, cada elemento a
ij representa o número de pessoas que saíram do ônibus
i e, após a parada, entraram no ônibus j.

Então, é correto concluir que,
 , nas incógnitas x e y, é impossível para valores de
(m, n) cuja representação no plano cartesiano de eixos ortogonais é uma
, nas incógnitas x e y, é impossível para valores de
(m, n) cuja representação no plano cartesiano de eixos ortogonais é uma , nas incógnitas x e y, é impossível para valores de
(m, n) cuja representação no plano cartesiano de eixos ortogonais é uma
, nas incógnitas x e y, é impossível para valores de
(m, n) cuja representação no plano cartesiano de eixos ortogonais é uma cujo determinante é igual a 8.
Nessas condições, o determinante da matriz 2A será igual a
cujo determinante é igual a 8.
Nessas condições, o determinante da matriz 2A será igual a 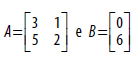 , tem
como soma de seus elementos o valor:
, tem
como soma de seus elementos o valor:  e B =[5 8]. A matriz X que satisfaz a equação matricial XA = B
tem elementos cuja soma é
e B =[5 8]. A matriz X que satisfaz a equação matricial XA = B
tem elementos cuja soma é 
 representam:
representam:
 obtendo-se a matriz
codificada B.A.
obtendo-se a matriz
codificada B.A. , podemos afirmar que a soma dos elementos da matriz
, podemos afirmar que a soma dos elementos da matriz  e sabendo que a matriz
e sabendo que a matriz  é a matriz inversa da matriz
é a matriz inversa da matriz  e sabendo que a matriz
e sabendo que a matriz  é a matriz inversa da matriz
é a matriz inversa da matriz  possui
infinitas soluções (x,y) para k igual a
possui
infinitas soluções (x,y) para k igual a