Uma empresa vende três produtos P1
, P2
e P3 cujos preços de venda, em unidades monetárias,
estão respectivamente representados pelos termos a1j, j ∈{1, 2, 3}, da matriz A= (63 90 70); o número
de unidades de cada produto, vendidas em um determinado mês está representado pelos termos
b1j, j ∈{1, 2, 3}, da matriz B = (45 25 35), e o custo de produção de cada produto, está representado
pelos termos c1j, j ∈{1, 2, 3}, da matriz C = (55 70 58).
Com base nessas informações, é correto afirmar:
O lucro total obtido com a venda dos três produtos foi igual a 1 240 unidades monetárias.



 respeitam a seguinte lei de formação para os seus
respeitam a seguinte lei de formação para os seus 


 e C=
e C=  , sendo m um número real. Sabendo que
C = A · B, então det C é igual a
, sendo m um número real. Sabendo que
C = A · B, então det C é igual a ,
quadrada de ordem 3, pode-se afirmar
,
quadrada de ordem 3, pode-se afirmar



 é simétrica.
é simétrica.  é simétrica
é simétrica é
é 
 corresponde à média
corresponde à média  , pelo eixo
, pelo eixo  é
é 
 , em que A
, em que A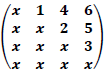 considere p(
considere p(