As coordenadas de um ponto P, no plano cartesiano, são
(a,b) = (1,1).  é uma matriz de rotação, P’ = M × P. Assinale a alternativa que apresenta as
coordenadas de P’, para α = π/
6.
é uma matriz de rotação, P’ = M × P. Assinale a alternativa que apresenta as
coordenadas de P’, para α = π/
6.
As coordenadas de um ponto P, no plano cartesiano, são
(a,b) = (1,1).  é uma matriz de rotação, P’ = M × P. Assinale a alternativa que apresenta as
coordenadas de P’, para α = π/
6.
é uma matriz de rotação, P’ = M × P. Assinale a alternativa que apresenta as
coordenadas de P’, para α = π/
6.




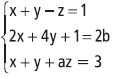 , sendo a e b números reais.
, sendo a e b números reais.






 , sendo k um número
real, com k < 2, B = (b
, sendo k um número
real, com k < 2, B = (b

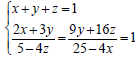 , em que
5 - 4z
, em que
5 - 4z 





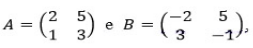 o produto entre a matriz inversa de A e a matriz transposta de B é a matriz
o produto entre a matriz inversa de A e a matriz transposta de B é a matriz 





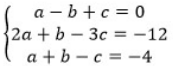 , então
, então 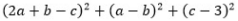 vale
vale 
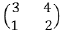 , o determinante de A
, o determinante de A sendo a, b,c e d números reais. As retas r: y = ax + b e s: y = cx + d são perpendiculares entre si, a
reta r contém o ponto (2, 3) e a reta s contém o
ponto (0,0). Assim, o determinante da
matriz A é
sendo a, b,c e d números reais. As retas r: y = ax + b e s: y = cx + d são perpendiculares entre si, a
reta r contém o ponto (2, 3) e a reta s contém o
ponto (0,0). Assim, o determinante da
matriz A é