Questõessobre Álgebra Linear - Equações Lineares, Espaço Vetorial e Transformações Lineares e Matrizes
Um grupo de cinco amigos resolveu passar o final de semana em um hotel fazenda no interior do estado de São Paulo.
Todos foram juntos no mesmo carro e decidiram dividir, igualmente, a despesa total da viagem entre os cinco participantes.
Dados da viagem de carro:
• a distância percorrida ida e volta foi de 432 km;
• o consumo de gasolina do veículo foi de 9 km/L;
• o preço da gasolina foi de R$ 4,50/L;
• o valor de cada pedágio foi de
o P1: R$ 10,00
o P2: R$ 2,50
o P3: R$ 4,40
o P4: R$ 2,70
Sabendo que todos os pedágios foram pagos na ida e na volta, cada amigo gastou em transporte, considerando
apenas a gasolina e os pedágios, a quantia de
A sistematização das notas musicais permitiu a padronização dos instrumentos e, com isso, a universalização da composição
musical desde o período renascentista.
O método adotado para a criação das notas foi o de construir uma sequência de frequências de sons conforme uma
Progressão Geométrica.
Um músico adota a frequência de Dó (1º
termo) em 261 Hz, e após 12 intervalos, obtém o próximo Dó (13º
termo) em
522 Hz, como vemos na tabela.

Esse músico deseja afinar seu instrumento utilizando a frequência da nota Lá (10º termo). A frequência que ele deverá
utilizar, em hertz, é igual a

Câmeras de vídeo funcionam basicamente tirando uma sequência de fotografias (chamadas de
“quadros”) em alta velocidade, em intervalos regulares, e quando essas imagens são exibidas
rapidamente nossos olhos percebem-nas como objetos em movimento. Existem 3 padrões
principais de vídeo no mundo: as câmeras de cinema, que fazem 24 quadros por segundo; as
câmeras de TV NTSC (padrão americano), que fazem 30 quadros por segundo; e as TV PAL
(padrão europeu) que fazem 25 quadros por segundo.
Supondo que três câmeras, uma de cada padrão mencionado, comecem a filmar exatamente
no mesmo instante, gerando o primeiro quadro idêntico, analise as proposições.
I. Após 1/6 de segundo de filmagem, as câmeras do padrão de cinema e de TV NTSC geram
o segundo quadro idêntico.
II. Após 10 segundos de filmagem, as três câmeras geram o segundo quadro idêntico.
III. Após 1 segundo de filmagem, as câmeras do padrão TV PAL e cinema gerarão o segundo
quadro idêntico.
IV. Após uma hora de filmagem, as câmeras de TV de padrão PAL e NTSC irão gerar 18001
quadros idênticos.
V. As três câmeras nunca irão gerar um segundo quadro idêntico.
Das proposições tem-se exatamente:
Num teste de esforço físico, o movimento de um
indivíduo caminhando em uma esteira foi
registrado por um computador. A partir dos
dados coletados, foi gerado o gráfico da
distância percorrida, em metros, em função do
tempo, em minutos, mostrado ao lado:
De acordo com esse gráfico, considere as
seguintes afirmativas:
1. A velocidade média nos primeiros 4
minutos foi de 6 km/h.
2. Durante o teste, a esteira permaneceu
parada durante 2 minutos.
3. Durante o teste, a distância total percorrida
foi de 1200 m.
Assinale a alternativa correta.

Num teste de esforço físico, o movimento de um indivíduo caminhando em uma esteira foi registrado por um computador. A partir dos dados coletados, foi gerado o gráfico da distância percorrida, em metros, em função do tempo, em minutos, mostrado ao lado: De acordo com esse gráfico, considere as seguintes afirmativas:
1. A velocidade média nos primeiros 4 minutos foi de 6 km/h.
2. Durante o teste, a esteira permaneceu parada durante 2 minutos.
3. Durante o teste, a distância total percorrida foi de 1200 m.
Assinale a alternativa correta.

Sobre sistemas de equações lineares 3 x 3, é verdadeiro que
Um ponto P, de coordenadas (x, y) do plano cartesiano ortogonal,
é representado pela matriz coluna  , assim como a
matriz coluna
, assim como a
matriz coluna  representa, no plano cartesiano ortogonal,
o ponto P de coordenadas (x, y).
representa, no plano cartesiano ortogonal,
o ponto P de coordenadas (x, y).
Sendo assim, o resultado da multiplicação matricial
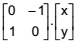 é uma matriz coluna que, no plano cartesiano
ortogonal, necessariamente representa um ponto que é
é uma matriz coluna que, no plano cartesiano
ortogonal, necessariamente representa um ponto que é
Um ponto P, de coordenadas (x, y) do plano cartesiano ortogonal,
é representado pela matriz coluna  , assim como a
matriz coluna
, assim como a
matriz coluna  representa, no plano cartesiano ortogonal,
o ponto P de coordenadas (x, y).
representa, no plano cartesiano ortogonal,
o ponto P de coordenadas (x, y).
Sendo assim, o resultado da multiplicação matricial
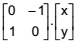 é uma matriz coluna que, no plano cartesiano
ortogonal, necessariamente representa um ponto que é
é uma matriz coluna que, no plano cartesiano
ortogonal, necessariamente representa um ponto que é
Seja F : R3 → R a função definida por F(x, y, z) = x2 + 4y2 – z2 , é correto afirmar:
O plano tangente à superfície F(x, y, z) = 1, no ponto (1, 1, 2), pode ser representado pela equação
x + y – z – 1 = 0.
Seja F : R3 → R a função definida por F(x, y, z) = x2 + 4y2 – z2 , é correto afirmar:
O plano tangente à superfície F(x, y, z) = 1, no ponto (1, 1, 2), pode ser representado pela equação
x + y – z – 1 = 0.
Seja F : R3 → R a função definida por F(x, y, z) = x2 + 4y2 – z2
, é correto afirmar:
A curva de equação  está contida na superfície F(x, y, z) = 1.
está contida na superfície F(x, y, z) = 1.
Seja F : R3 → R a função definida por F(x, y, z) = x2 + 4y2 – z2 , é correto afirmar:
A curva de equação  está contida na superfície F(x, y, z) = 1.
está contida na superfície F(x, y, z) = 1.
Considerando-se, no espaço R3 , os pontos A = (1, 2, 1), B = (2, 0, 2), C = (4, k, 4) e o plano α de equação x – 2y + 2z + 4 = 0, é correto afirmar:
Se a base de um cone circular, de raio 3u.c., está contida no plano α e o vértice do cone é o ponto A,
então o seu volume é 3π u.v..
Considerando-se, no espaço R3 , os pontos A = (1, 2, 1), B = (2, 0, 2), C = (4, k, 4) e o plano α de equação x – 2y + 2z + 4 = 0, é correto afirmar:
Se a base de um cone circular, de raio 3u.c., está contida no plano α e o vértice do cone é o ponto A,
então o seu volume é 3π u.v..
Considerando-se, no espaço R3 , os pontos A = (1, 2, 1), B = (2, 0, 2), C = (4, k, 4) e o plano α de equação x – 2y + 2z + 4 = 0, é correto afirmar:
O vetor  é ortogonal ao plano α.
é ortogonal ao plano α.
Considerando-se, no espaço R3 , os pontos A = (1, 2, 1), B = (2, 0, 2), C = (4, k, 4) e o plano α de equação x – 2y + 2z + 4 = 0, é correto afirmar:
O vetor  é ortogonal ao plano α.
é ortogonal ao plano α.