Os tempos estão mudando, a beleza já não
segue um único padrão, e os concursos de Miss
Mundo afora são exemplos disso. A participação de
uma candidata com a prótese de perna no concurso
de Miss Itália 2018 foi o retrato dessa diversidade.

Disponível em: <https://istoe.com.br/conheca-as-finalistas-do-miss-italia-2018/>. Acesso em: nov. 2018.
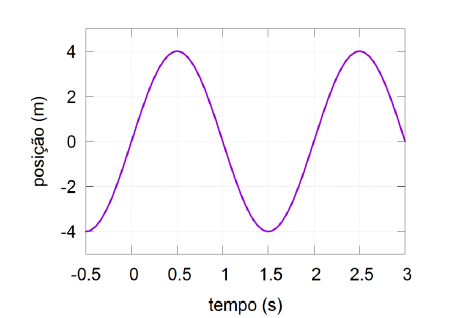
A figura representa o modelo de um oscilador massa-mola,
que é composto por uma mola com constante elástica k de
massa desprezível e um bloco de massa m, apoiado em uma
superfície horizontal, que fundamenta um dos princípios de
funcionamento de uma prótese para membros inferiores,
pois o movimento oscilatório que surge do ato de caminhar
e das forças restauradoras que tendem a trazer ou manter
o sistema em determinado estado ou posição assemelha-se
ao do oscilador harmônico.
Sobre o comportamento do oscilador harmônico simples,
desprezando-se o atrito do bloco com a superfície de apoio,
é correto afirmar:











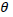 com a vertical e posteriormente é
liberado do repouso.
com a vertical e posteriormente é
liberado do repouso.




