Questõessobre Máquina de Atwood e Associação de Blocos

InícioTodas as questões
1
1
Foram encontradas 35 questões
68d8eab0-fd
UFT 2018 - Física - Estática e Hidrostática, Máquina de Atwood e Associação de Blocos, Dinâmica, Leis de Newton, Estática - Momento da Força/Equilíbrio e Alavancas

Atualmente um dos câmbios mais modernos utilizados na indústria automotiva é o cambio CVT (Continuosly Variable Transmission) onde a transmissão varia continuamente. O funcionamento básico consiste em duas polias cônicas ligadas por uma correia. Elas variam o seu diâmetro de acordo com a necessidade exigida pelo condutor. Se for necessária uma força maior, como por exemplo quando o veículo precisa vencer uma subida, a polia que liga o eixo de transmissão de torque às rodas fica com o diâmetro maior e a polia ligada à rotação do motor assume um diâmetro menor. O tempo TR corresponde a uma volta completa da polia maior e Tr refere-se ao tempo de uma volta completa da polia menor. Supondo-se que nesta situação a polia menor tem 2/3do diâmetro da polia maior, e que a correia que liga as duas polias não desliza, o tempo Tr necessário para que a polia menor dê uma volta completa é

A
Tr = 2/3 TR
B
Tr= 3/2 TR
C
Tr= 2 TR
D
Tr = 3 TR
a53940fe-00
UEMG 2019 - Física - Máquina de Atwood e Associação de Blocos, Dinâmica, Leis de Newton

Dois blocos A e B de massas respectivamente iguais à mA e mB são ligados por uma corda de massa desprezível que passa por uma roldana fixa, tal como representado na figura. Considere que nessa situação não existem forças de atrito atuando no sistema.



O diagrama que representa corretamente as forças que atuam sobre o bloco A é

A

B

C

D

d4fdef5a-fc
PUC - RS 2018 - Física - Oscilação e Ondas, Máquina de Atwood e Associação de Blocos, Dinâmica, Leis de Newton, Ondas e Propriedades Ondulatórias

A força tensora sobre uma corda e a sua densidade linear são aspectos relevantes para que se possa determinar o valor da velocidade de propagação de um pulso mecânico nesse meio. Na expressão abaixo, FT representa a força tensora na corda, µ a densidade linear do meio e v a velocidade de propagação do pulso na corda.


Para a situação de uma corda instalada, como mostra a figura abaixo, assuma que o comprimento de onda seja muito maior do que o deslocamento transversal máximo.



Considere que inicialmente uma força tensora de intensidade F esteja aplicada ao cabo, produzindo uma onda estacionária de frequência ƒ e comprimento de onda λ. Para se obter uma frequência três vezes maior para a onda na mesma corda, mantendo-se constante o seu comprimento de onda, seria necessário aumentar a massa do bloco _________, e o som produzido seria mais _________.

A
3 vezes – grave
B
3 vezes – agudo
C
9 vezes – grave
D
9 vezes – agudo
cb7e2786-f8
PUC - RJ 2019 - Física - Plano Inclinado e Atrito, Máquina de Atwood e Associação de Blocos, Dinâmica, Leis de Newton

Dois corpos estão ligados, como na figura, sendo a aceleração do sistema igual a g/10, onde g é a aceleração da gravidade. O corpo 1, que está pendente, tem massa M. O corpo 2, que se move em uma mesa horizontal, tem massa 4M.

Calcule o coeficiente de atrito cinético entre o corpo 2 e a mesa.


A
0,125
B
0,250
C
0,500
D
1,00
E
4,00
87b18512-f8
PUC - RJ 2019 - Física - Plano Inclinado e Atrito, Máquina de Atwood e Associação de Blocos, Dinâmica, Leis de Newton

Seja o sistema mostrado na figura. A caixa 2, de massa m2 = 2,0 kg, está descendo com velocidade constante e igual a 1,5 m/s. O coeficiente de atrito cinético entre a caixa 1 e a mesa que a sustenta é 0,4.

Qual é a massa da caixa 1, em kg?


Dado

aceleração da gravidade g = 10 m/s²

A
1,5
B
2,0
C
3,0
D
4,0
E
5,0
f58cc309-e3
UCPEL 2018 - Física - Máquina de Atwood e Associação de Blocos, Dinâmica

Em uma atividade experimental, estudantes desenvolveram um teste para estimar o valor do coeficiente de atrito estático entre duas superfícies. O aparato experimental, que possui um corpo A apoiado em uma superfície horizontal e um corpo B suspenso é ilustrado na figura abaixo.


O teste consiste em determinar o coeficiente de atrito estático entre a superfície do corpo A e a superfície em que ele está apoiado e, para tal, o arranjo permite que a massa do corpo B, suspenso, seja alterada em intervalos de 0,05kg. Os estudantes apresentaram os dados experimentais na tabela abaixo:


Sabendo-se que o módulo da aceleração da gravidade é igual a 10m/s² e que a massa do corpo A é igual a 6,0kg, o valor estimado para o coeficiente de atrito estático é igual a:

A
0,35
B
0,30
C
0,20
D
0,15
E
0,25
b65a7d89-b8
UECE 2013 - Física - Máquina de Atwood e Associação de Blocos, Dinâmica, Leis de Newton

Dois cubos de mesma densidade e tamanhos diferentes repousam sobre uma mesa horizontal e mantêm contato entre si por uma de suas faces. A aresta de um dos cubos mede o dobro da aresta do outro. Em um dado instante, uma força constante , horizontal, é aplicada sobre o cubo menor que, por sua vez, empurra o maior, conforme a figura a seguir.


Despreze todos os atritos. A razão entre o módulo de e o módulo da força de contato entre os cubos é

A
8.
B
2.
C
1/8.
D
9/8.
33b3c0c2-d8
EINSTEIN 2018 - Física - Máquina de Atwood e Associação de Blocos, Dinâmica, Leis de Newton

Um bloco de massa m = 4 kg é mantido em repouso, preso a uma corda de densidade linear de massa µ = 4 × 10–3 kg/m, que tem sua outra extremidade fixa no ponto A de uma parede vertical. Essa corda passa por uma roldana ideal presa em uma barra fixa na parede, formando um ângulo de 60º com a barra. Considere que um diapasão seja colocado para vibrar próximo desse sistema e que ondas estacionárias se estabeleçam no trecho AB da corda.

Sabendo que a velocidade de propagação de uma onda por uma corda de densidade linear de massa μ, submetida a uma força de tração T, é dada por v = , que g = 10 m/s2 , que cos 60º = sen 30º = 0,5 e considerando as informações da figura, pode-se afirmar que a frequência fundamental de ondas estacionárias no trecho AB da corda é

A
56 Hz.
B
50 Hz.
C
35 Hz.
D
48 Hz.
E
40 Hz.
0ddcc367-ef
Inatel 2019 - Física - Máquina de Atwood e Associação de Blocos, Dinâmica, Leis de Newton

Na construção civil, é comum encontrarmos sistemas de roldanas empregados na realização de tarefas. Você precisa erguer uma caixa de argamassa até os andares superiores de um prédio em construção. Para isso, você utiliza uma corda e uma roldana que juntos suportam, no máximo, uma tensão de 600 N, para atender a essa exigência uma carga de 50 kg deverá ser elevada com uma aceleração máxima de:

A
5,0 m/s²
B
3,6 m/s²
C
2,00 m/s²
D
1,50 m/s²
E
1,00 m/s²
50f66750-e7
UEFS 2009 - Física - Plano Inclinado e Atrito, Máquina de Atwood e Associação de Blocos, Dinâmica, Leis de Newton, Trabalho e Energia, Energia Mecânica e sua Conservação



Um motor com rendimento de 70% puxa um bloco de 50,0kg, que desliza com velocidade constante de 5,0m/s sobre o plano inclinado representado na figura.

Desprezando-se a resistência do ar, admitindo-se as polias e o fio como sendo ideais, o módulo da aceleração da gravidade, g = 10,0m/s2 , o coeficiente de atrito dinâmico, µd = 0,3, e sabendo-se que cos = 0,8 e sen = 0,6, a potência do motor, em kW, é igual a

A
2,1
B
3,0
C
4,5
D
5,1
E
6,0
de7bc322-e1
UCPEL 2007 - Física - Oscilação e Ondas, Máquina de Atwood e Associação de Blocos, Dinâmica, Energia Mecânica e sua Conservação, Ondas e Propriedades Ondulatórias

Um experimento físico comumente usado para mostrar ondas estacionárias numa corda fixa nas duas extremidades é mostrado na figura abaixo. Consiste em um peso preso na extremidade de uma corda que passa por uma roldana; a outra extremidade da corda é presa a um oscilador mecânico que movimenta a corda para cima e para baixo em uma dada freqüência f. O comprimento L entre o oscilador e a roldana é fixo.


Podemos afirmar que

A
se aumentarmos o peso P sem alterarmos a freqüência f, a velocidade de propagação da onda na corda não se altera.
B
o comprimento de onda da onda estacionária na corda é L.
C
o comprimento de onda da onda estacionária na corda é L/4.
D
o comprimento de onda da onda estacionária na corda é L/2.
E
se dobrarmos a freqüência f do oscilador mecânico, o número de ventres reduzir-se-á à metade.
07d6beaa-b4
UEFS 2010 - Física - Oscilação e Ondas, Máquina de Atwood e Associação de Blocos, Dinâmica, Leis de Newton, Trabalho e Energia, Movimento Harmônico

Observa-se que quatro passageiros, cuja massa total é de 300,0kg, comprimem 30,0cm as molas de um automóvel quando entram nele.

Sabendo-se que a massa do automóvel é 600,0kg, o período de vibração do automóvel carregado, em πs, é igual a

A
0,8
B
0,7
C
0,6
D
0,5
E
0,4
e146cca4-b0
UNICENTRO 2010 - Física - Oscilação e Ondas, Plano Inclinado e Atrito, MCU - Movimento Circular Uniforme, Cinemática Vetorial, Máquina de Atwood e Associação de Blocos, Dinâmica, Leis de Newton, Cinemática, Impulso e Quantidade de Movimento, Movimento Harmônico

Analise as alternativas e assinale a correta.

A
No movimento circular uniforme a força centrípeta equilibra a força centrífuga.
B
Impulso é sinônimo de Quantidade de Movimento.
C
O trabalho de forças externas que agem sobre um sólido é igual ao incremento de sua energia cinética.
D
No movimento oscilatório de um pêndulo simples são feitos percursos iguais em tempos iguais, portanto, o movimento pendular é uniforme.
E
Na máquina de Atwood, a força de tração no fio é igual ao peso do sólido suspenso de maior massa.
111e4ca2-cc
IF-RR 2018 - Física - Máquina de Atwood e Associação de Blocos, Dinâmica, Leis de Newton

Os blocos A e B de massas iguais a 10 kg e 20 kg, respectivamente, estão interligados por um fio leve e apoiados em um piso horizontal. O bloco B é puxado por uma força de 600 N. Desprezando o atrito, qual é a intensidade da força tensora no fio que une os blocos?



A
400 N
B
500 N
C
300 N
D
100 N
E
200 N
b1996c8b-ce
IF Sul - MG 2018 - Física - Máquina de Atwood e Associação de Blocos, Dinâmica

Duas caixas de massa m1 e m2 são empurradas ao longo de uma superfície horizontal sem atrito por uma força horizontal de acordo com a figura abaixo. O módulo da força de contato entre as caixas é de:


A
m2F/(m1 + m2)
B
m2 F/m1
C
m2F/(m1 – m2)
D
m1F/(m1 + m2)
24d3ded3-cb
UDESC 2018 - Física - Máquina de Atwood e Associação de Blocos, Dinâmica

A Figura 3 mostra dois blocos de massa M e m, unidos por um fio ideal, suspensos por um sistema de polias ideais.



Assinale a alternativa que corresponde à condição de equilíbrio.

A
M=6m
B
M=8m
C
M=4m
D
M=2m
E
M=m
852b6bc9-c0
PUC - PR 2016 - Física - Máquina de Atwood e Associação de Blocos, Dinâmica

Um bloco A de massa 3,0 kg está apoiado sobre uma mesa plana horizontal e preso a uma corda ideal. Acorda passa por uma polia ideal e na sua extremidade final existe um gancho de massa desprezível, conforme mostra o desenho. Uma pessoa pendura, suavemente, um bloco B de massa 1,0 kg no gancho. Os coeficientes de atrito estático e cinético entre o bloco A e a mesa são, respectivamente, µe = 0,50 e µc =0,20. Determine a força de atrito que a mesa exerce sobre o bloco A. Adote g = 10 m/s²


A
15 N.
B
6,0 N.
C
30 N.
D
10 N.
E
12 N.
530a827d-36
CEDERJ 2016 - Física - Máquina de Atwood e Associação de Blocos, Dinâmica

Três caixas são empurradas por uma força horizontal, de intensidade F, sobre uma mesa, conforme ilustrado na figura.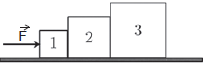
                                
                                                                       

Considere que o atrito entre as caixas e a mesa é desprezível, e que as intensidades das forças entre as caixas 1 e 2 é N1 e entre as caixas 2 e 3 é N2 . Nesse caso, a relação entre F, N1 e N2 é dada por

A

F = N1 = N2

B
F > N1 = N2
C
F < N1 < N2
D
F > N1 > N2
c14efb8e-1c
PUC - SP 2015 - Física - Máquina de Atwood e Associação de Blocos, Dinâmica

Em uma máquina de Atwood ideal, são presas duas massas, tais que M1 >M2. Inicialmente as massas estão em repouso e niveladas. Após o abandono simultâneo das massas, verifica-se que a energia total do sistema é de 100J, após elas terem percorrido 5m em 2s, alcançando uma velocidade de 5,0m/s. Sabendo que o módulo da aceleração da gravidade é de 10m/s2 , determine, em kg, os valores de cada uma das massas.


A
M1=6,0 e M2=2,0
B
M1=6,5 e M2=1,5
C
M1=4,5 e M2=3,5
D
M1=5,0 e M2=3,0
e93a14b7-94
UNESP 2011 - Física - Máquina de Atwood e Associação de Blocos, Dinâmica

Considerando g = 10 m/s2, desprezando os efeitos do ar sobre o sistema e os atritos durante o movimento acelerado, a massa M, em kg, do corpo que deve ser colocado na plataforma B para acelerar para cima a massa m no intervalo de 3 s é igual a

Em uma obra, para permitir o transporte de objetos para cima, foi montada uma máquina constituída por uma polia, fios e duas plataformas A e B horizontais, todos de massas desprezíveis, como mostra a figura.
Um objeto de massa m = 225 kg, colocado na plataforma A, inicialmente em repouso no solo, deve ser levado verticalmente para cima e atingir um ponto a 4,5 m de altura, em movimento uniformemente acelerado, num intervalo de tempo de 3 s.
A partir daí, um sistema de freios passa a atuar, fazendo a plataforma A parar na posição onde o objeto será descarregado.
A
275.
B
285.
C
295.
D
305.
E
315.