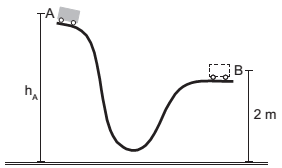
Os grandes parques de diversões espalhados pelo mundo são destinos tradicionais de férias das famílias brasileiras. Considere um perfil de montanha-russa mostrado na imagem, na qual o looping possui um raio R. Desprezando qualquer forma de dissipação de energia no sistema e supondo que a energia cinética medida para o
carrinho seja apenas de translação, a altura mínima em relação ao nível de referência em que o carrinho pode
partir do repouso e efetuar o looping com sucesso é

Os grandes parques de diversões espalhados pelo mundo são destinos tradicionais de férias das famílias brasileiras. Considere um perfil de montanha-russa mostrado na imagem, na qual o looping possui um raio R. Desprezando qualquer forma de dissipação de energia no sistema e supondo que a energia cinética medida para o carrinho seja apenas de translação, a altura mínima em relação ao nível de referência em que o carrinho pode partir do repouso e efetuar o looping com sucesso é