Questõessobre Colisão

Em um jogo de sinuca, a bola A é lançada com velocidade V de módulo constante e igual a 2 m/s em uma direção paralela às tabelas (laterais) maiores da mesa, conforme representado na figura 1. Ela choca-se de forma perfeitamente elástica com a bola B, inicialmente em repouso, e, após a colisão, elas se movem em direções distintas, conforme a figura 2.

Sabe-se que as duas bolas são de mesmo material e idênticas em massa e volume. A bola A tem, imediatamente depois da colisão, velocidade de módulo igual a 1 m/s. Desprezando os atritos e sendo EꞌB a energia cinética da bola B imediatamente depois da colisão e EA a energia cinética da bola A antes da colisão, a razão é igual a

Na Copa do Mundo de 2018, observou-se que, para a maioria dos torcedores, um dos fatores que encantou foi o jogo bem jogado, ao passo que o desencanto ficou por conta de partidas com colisões violentas. Muitas dessas colisões travavam as jogadas e, não raramente, causavam lesões nos atletas. A charge a seguir ilustra a narração de um suposto jogo da Copa, feita por físicos:

Com base na charge e nos conhecimentos sobre colisões e supondo que, em um jogo de futebol, os jogadores se comportam como um sistema de partículas ideais, é correto afirmar que, em uma colisão

Considere a figura a seguir em que uma bola de massa m, suspensa na extremidade de um fio, é solta de uma altura h e colide elasticamente, em seu ponto mais baixo, com um bloco de massa 2m em repouso sobre uma superfície sem nenhum atrito. Depois da colisão, a bola subirá até uma altura igual a

Em uma mesa de sinuca, as bolas A e B, ambas com massa igual a 140 g, deslocam-se com velocidades VA e VB, na mesma direção e sentido. O gráfico abaixo representa essas velocidades ao longo do tempo.

Após uma colisão entre as bolas, a quantidade de movimento total, em kg.m/s, é igual a:

Uma caminhonete, de massa 2.000 kg, bateu na traseira de um sedã, de massa 1.000 kg, que estava parado no semáforo, em uma rua horizontal. Após o impacto, os dois veículos deslizaram como um único bloco. Para a perícia, o motorista da caminhonete alegou que estava a menos de 20 km/h quando o acidente ocorreu. A perícia constatou, analisando as marcas de frenagem, que a caminhonete arrastou o sedã, em linha reta, por uma distância de 10 m. Com este dado e estimando que o coeficiente de atrito cinético entre os pneus dos veículos e o asfalto, no local do acidente, era 0,5, a perícia concluiu que a velocidade real da caminhonete, em km/h, no momento da colisão era, aproximadamente,

Aceleração da gravidade: 10 m/s2 .

Desconsidere a massa dos motoristas e a resistência do ar.

A lei de conservação do momento linear está associada às relações de simetrias espaciais.

Nesse contexto, considere uma colisão inelástica entre uma partícula de massa M e velocidade V e um corpo, inicialmente em repouso, de massa igual a 10M.

Logo após a colisão, a velocidade do sistema composto pela partícula e pelo corpo equivale a:

INSTRUÇÃO: Para responder à questão, analise a situação a seguir.

Duas esferas – A e B – de massas respectivamente iguais a 3 kg e 2 kg estão em movimento unidimensional sobre um plano horizontal perfeitamente liso, como mostra a figura 1.

Figura 1:

Inicialmente as esferas se movimentam em sentidos opostos, colidindo no instante t1 . A figura 2 representa a evolução das velocidades em função do tempo para essas esferas imediatamente antes e após a colisão mecânica.

Figura 2:

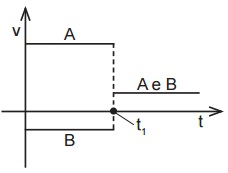
Sobre o sistema formado pelas esferas A e B, é correto afirmar:

VEÍCULO ARRASTADO POR TREM EM FORTALEZA 

https://dialogospoliticos.wordpress.com (adaptado). Acesso: 02/04/2016

A figura mostra uma colisão envolvendo um trem de carga e uma camionete. Segundo testemunhas, o condutor da camionete teria ignorado o sinal sonoro e avançou a cancela da passagem de nível. Após a colisão contra a lateral do veículo, o carro foi arrastado pelo trem por cerca de 300 metros. Supondo a massa total do trem de 120 toneladas e a da camionete de 3 toneladas, podemos afirmar que, no momento da colisão, a intensidade da força que 

Um objeto de massa m escorrega com velocidade V sobre uma superfície horizontal sem atrito e colide com um objeto de massa M que estava em repouso. Após a colisão, os dois objetos saem grudados com uma velocidade horizontal igual a V/4.

Calcule a razão M/m.

Tempestades solares são causadas por um fluxo intenso de partículas de altas energias ejetadas pelo Sol durante erupções solares. Esses jatos de partículas podem transportar bilhões de toneladas de gás eletrizado em altas velocidades, que podem trazer riscos de danos aos satélites em torno da Terra.

Considere que, em uma erupção solar em particular, um conjunto de partículas de massa total mp = 5 kg, deslocando-se com velocidade de módulo vp = 2x105 m/s, choca-se com um satélite de massa Ms = 95 kg que se desloca com velocidade de módulo igual a Vs = 4x103 m/s na mesma direção e em sentido contrário ao das partículas. Se a massa de partículas adere ao satélite após a colisão, o módulo da velocidade final do conjunto será de

Considere um patinador X que colide elasticamente com a parede P de uma sala. Os diagramas abaixo mostram segmentos orientados indicando as possíveis forças que agem no patinador e na parede, durante e após a colisão. Note que segmento nulo indica força nula.

Supondo desprezível qualquer atrito, o diagrama que melhor representa essas forças é designado por:

Admita uma colisão frontal totalmente inelástica entre um objeto que se move com velocidade inicial v0 e outro objeto inicialmente em repouso, ambos com mesma massa.

Nessa situação, a velocidade com a qual os dois objetos se movem após a colisão equivale a:

Uma massa de 10 g e velocidade inicial de 5,0 m/s colide, de modo totalmente inelástico, com outra massa de 15 g que se encontra inicialmente em repouso.

O módulo da velocidade das massas, em m/s, após a colisão é: