0fb5a197-04
FGV 2020 - Matemática - Probabilidade
A figura indica a planificação de dois dados cúbicos e honestos utilizados em um jogo.

Na sua jogada, um jogador lança aleatoriamente o dado A e, em seguida, o dado B. Após os
lançamentos, ele precisa escolher um resultado entre duas opções:
I. somar os números das faces que ficaram voltadas para cima dos dois dados;
II. subtrair os números das faces que ficaram voltadas para baixo dos dois dados e pegar o
módulo do resultado.
Se em uma jogada o dado A ficou com a face do número 1/6 voltada para cima, a probabilidade
de que, após lançar o dado B, o jogador dessa jogada possa fazer uma escolha de resultado
que corresponda a um número entre 1 e 2 é igual a
A figura indica a planificação de dois dados cúbicos e honestos utilizados em um jogo.

Na sua jogada, um jogador lança aleatoriamente o dado A e, em seguida, o dado B. Após os
lançamentos, ele precisa escolher um resultado entre duas opções:
I. somar os números das faces que ficaram voltadas para cima dos dois dados;
II. subtrair os números das faces que ficaram voltadas para baixo dos dois dados e pegar o
módulo do resultado.
Se em uma jogada o dado A ficou com a face do número 1/6 voltada para cima, a probabilidade
de que, após lançar o dado B, o jogador dessa jogada possa fazer uma escolha de resultado
que corresponda a um número entre 1 e 2 é igual a
A
5/6
B
2/3
C
1/2
D
1/3
E
1/6

 do triângulo isósceles FGV são F(6, 0) e
G(0, 6). Sendo m e n os dois valores possíveis de abscissa de V para que a área de FGV seja
igual a 6 unidades de área do plano cartesiano, o valor de m + n é
do triângulo isósceles FGV são F(6, 0) e
G(0, 6). Sendo m e n os dois valores possíveis de abscissa de V para que a área de FGV seja
igual a 6 unidades de área do plano cartesiano, o valor de m + n é





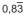
 . Sabe-se que PC = PA = k e que PB = 5, em unidades de
comprimento.
. Sabe-se que PC = PA = k e que PB = 5, em unidades de
comprimento. 






 e
e  ,
indicadas por m e n, intersectam-se no ponto C, que é centro da circunferência λ, de raio
CE = CF, como mostra a figura.
,
indicadas por m e n, intersectam-se no ponto C, que é centro da circunferência λ, de raio
CE = CF, como mostra a figura.