Vetores: o que são, como calcular e como caem no Enem

Um vetor pode ser representado conforme as seguintes direções: vertical, horizontal e diagonal. Os sentidos se apresentam após definida à direção do vetor: da direita para esquerda, da esquerda para direita, de cima para baixo e de baixo para cima, de baixo para cima e de cima para baixo.

Vejamos as imagens abaixo:

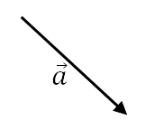
O vetor a está na direção diagonal e no sentido de cima para baixo e da esquerda para direita, enquanto o vetor c:

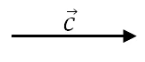
Está na direção horizontal e no sentido da esquerda para direita.

Os vetores são setas utilizadas para representar as grandezas físicas vetoriais que necessitam de uma orientação, ou seja, de direção e sentido bem definidos para sua efetiva aplicação nos problemas físicos. Imagine o avião que desenvolve uma velocidade escalar média do sul da América latina para em direção ao norte. O vetor velocidade que representa e define geometricamente essa grandeza física(velocidade) deve estar orientado na vertical para cima, como mostra a imagem a seguir:

Propriedades dos vetores

Os vetores, além de direção e sentido, também precisam de módulo e de uma unidade de medida. O módulo representa a intensidade do vetor, ou seja, o seu valor numérico, já a unidade de medida refere-se ao estudo dimensional da grandeza física a que o vetor representa. Veja a imagem a seguir:

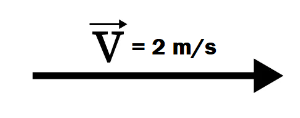
O vetor velocidade ilustrado representa uma velocidade de 2 m/s. Podemos interpretar que a velocidade tem módulo de 2, sua unidade de medida é o metro por segundo e a sua orientação é dada pela direção horizontal e sentido da esquerda para direita.

Podemos calcular o valor de um vetor através da soma de vetores. Logo, os vetores podem ser aplicados em operações matemáticas, a mais comum é a soma de vetores, onde todas as informações descritas até aqui sobre os vetores são fundamentais para executar as operações.

Operações com vetores

É importante lembrar que a soma de vetores não define que os vetores deverão ser sempre somados como em uma soma algébrica, em que 2 + 2 = 4. Dois vetores que possuem 2 unidades cada, mas que estão em direções opostas, não terão 4 unidades como resultado da soma vetorial. Vamos aprofundar a soma de vetores, dividindo nosso estudo nos 3 principais casos de soma vetorial.

Casos de soma vetorial

Vetores na mesma direção e com mesmo sentido.

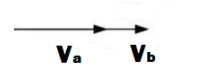
Os vetores Va e Vb ambos estão na horizontal e ambos estão para direita, considere que o vetor Va tem módulo de 5 m/s, assim como o Vb tem módulo de 10 m/s, logo a soma deles é dada por Va + Vb = 5 + 10 = 15 m/s. O vetor resultante é de 15 m/s, na mesma direção e mesmo sentido.

Vetores na mesma direção, mas com sentidos opostos.

Os vetores F1 e F2 ambos estão na horizontal, mas o vetor F1 está com sentido da direita para esquerda e o vetor F2 está com sentido da esquerda para direita. Considere que o vetor F1 tem módulo de 7N e o vetor F2 tem módulo de 12 N. Neste caso, para realizar a soma dos vetores, precisamos adotar um referencial para o sentido de cada vetor, vamos adotar o referencial do plano cartesiano, adotando assim o sinal negativa (-) para o vetor F1, logo a soma é dada por F1 + F2 = - 7 + 12 = + 5 N.

O vetor resultante é de + 5N, logo o vetor resultante encontra-se na mesma direção e com sentido orientado pelo sinal positivo (+), logo com sentido para direita.

Vetores em direções opostas.

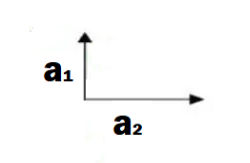
Os vetores a1 e a2 estão em direções opostas, o vetor a1 está na direção vertical enquanto o vetor a2 está na horizontal. Considere que o vetor a1 tem módulo de 2 m/s e o vetor a2 tem módulo de 2 m/s, diferente da soma algébrica, neste caso a soma vetorial não é dada pela simples soma dos módulos, devemos aplicar a regra do paralelogramo para encontrar a orientação do vetor aceleração resultante, assim como aplicar o teorema de Pitágoras para encontrar o módulo da aceleração resultante:

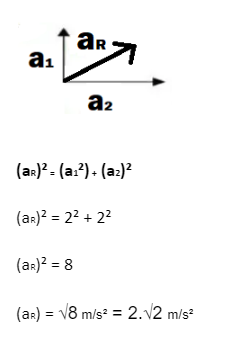
Grandezas vetoriais x escalares

As grandezas físicas vetoriais precisam de módulo, direção, sentido e unidade de medida, como já citamos. Na Física, os vetores representam grandezas vetoriais. As principais grandezas físicas vetoriais são: velocidade, escalar, quantidade de movimento, impulso, força, etc. As grandezas físicas escalares precisam apenas de módulo e unidade de medida para poderem ser interpretadas corretamente. As principais grandezas físicas escalares são: tempo, massa, comprimento, distância, energia, etc.

Vetores no Enem

Aprendemos a calcular vetores a depender de como estão os vetores somados. As principais grandezas físicas vetoriais citadas neste material são aplicadas em assuntos recorrentes no Enem, como, por exemplo, a cinemática: situações-problemas envolvendo o movimento de corpos através do desenvolvimento de uma velocidade ou atuação de uma aceleração.

Ainda dentro da cinemática, temos um tema bastante importante e presente nas últimas edições do ENEM: os lançamentos, questões de lançamento horizontal e oblíquo, que para determinarmos as velocidades na horizontal(Vx) e vertical(Vy) no lançamento oblíquo devemos saber aplicar o terceiro caso (III) aqui citado neste material, quando necessário. Podemos dizer que o estudo dos vetores no Enem é um assunto importante que o aluno deve focar durante a sua preparação. Outro conteúdo em que os conceitos de vetores são aplicados é em Estática e Dinâmica, situações em que os corpos estão em equilíbrio e precisamos analisar as forças que atuam em um corpo através da soma de vetores. Vejamos uma questão de vetores para exemplificar a abordagem do conteúdo:

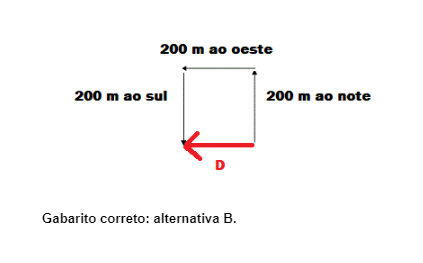
(UFMG) Uma pessoa sai para dar um passeio pela cidade, fazendo o seguinte percurso: sai de casa e anda 2 quarteirões para o Norte; dobra à esquerda andando mais 2 quarteirões para Oeste, virando, a seguir, novamente à esquerda e andando mais dois quarteirões para o Sul.

Sabendo que cada quarteirão mede 100m, o deslocamento da pessoa é:

a) 700m para Sudeste

b) 200m para Oeste

c) 200m para Norte

d) 700m em direções variadas

e) 0m

Ao ler o texto base da questão percebemos que a principal competência a ser interpretada é a direção dos vetores. A orientação dos vetores permitirá determinar que o deslocamento é dado pelo módulo e pela direção percorrida na situação problema, visto que o deslocamento é a distância percorrida em linha reta. O deslocamento percorrido na situação é de 200 metros para oeste.