Radiciação: o que é, propriedades, como resolver

A radiciação é uma operação matemática fruto de uma construção histórica. Podemos definir radiciação como o processo de “extrair” a raiz de um número, ou, a radiação é uma operação, onde a raiz representa uma potência com expoente fracionário. Por exemplo, a raiz quadrada de 25 é igual a 5. Isto acontece, pois 5² = 25, logo percebemos uma relação entre a operação de potenciação e radiciação. Estudaremos a operação de radiciação, suas peculiaridades e propriedades a seguir.

Símbolos, elementos e leitura da radiciação

Vamos agora definir os símbolos, elementos e a leitura da Radiciação. Antes de irmos para uma generalização, veja algumas radiciações a seguir:

Logo, podemos perceber que:

Algumas observações são necessárias. Primeiro: se a 0 e n é par ou ímpar, então b será uma número real positivo ou zero. Segundo: se a < 0, n for par, não existe a raiz b. Se a < 0, n for ímpar, a raiz b sempre será um número real negativo.

Propriedades da radiciação

Agora veremos as propriedades da radiciação.

Primeira propriedade

Dado um índice n e um radicando a, temos que:

Segunda propriedade

A raiz enésima de um produto é igual ao produto das raízes enésimas dos fatores. Vejamos alguns exemplos:

Terceira propriedade

A raiz enésima de um quociente é igual ao quociente das raízes enésimas dos termos da divisão.

Quarta propriedade

Multiplicando-se ou dividindo-se o índice de um radical e o expoente do radicando por um mesmo número p diferente de zero, o valor do radical não se altera.

Quinta propriedade

Se a é um número real positivo, m é um número inteiro e n é um número natural diferente de zero, então.

Sexta propriedade

Para se extrair a raiz de um radical, multiplicam-se os índices dos radicais e conserva-se o radicando.

Simplificação de radicais

Para a simplificação de radicais iremos utilizar as propriedades vistas acima e a técnica de fatoração. Você lembra o que é fatoração?

Fatorar é decompor um número em fatores primos, expressando estes fatores em forma de potência. Vamos agora à simplificação de radicais. Veja o exemplo a seguir:

Operações com radicais

As operações com radicais vamos agrupá-las em Adição e Subtração, Multiplicação e Divisão. Vejamos:

Adição e Subtração

A adição e subtração de radicais é realizada quando os radicais são semelhantes (mesmo índice e mesmo radicando). Exemplo:

Note que o radical não sofre alteração, no índice ou radicando.

Multiplicação e Divisão

A multiplicação e divisão de radicais ocorre quando os radicais tiverem o mesmo índice (utilizamos a segunda e terceira propriedades). Neste caso, basta multiplicarmos os radicando conservando o índice.

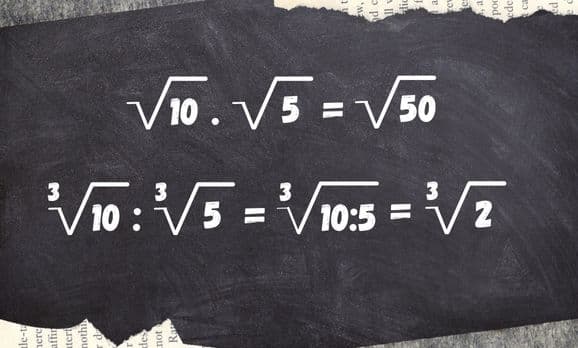
Radiciação e Potenciação

Radiciação e potenciação são operações inversas. Quando definimos que:

Estabelecemos aí uma relação entre a radiciação e potenciação. Ficando claro essa relação na quinta propriedade:

Radiciação no ENEM

No ENEM, a radiciação se apresenta de várias formas. Comparação de radicais, propriedades, simplificação etc. Analise o problema a seguir:

Calcule a expressão:

Para encontrar o valor da expressão vamos seguir alguns passos.