MMC: Mínimo Múltiplo Comum - O que é e como resolver

Denomina-se M.M.C (Mínimo Múltiplo Comum) de dois ou mais números inteiros o menor número inteiro que é múltiplo simultaneamente destes dois ou mais números. Para números inteiros temos múltiplos e divisores, onde o conjunto de múltiplos de um número é infinito diferente do conjunto dos divisores que é finito.

Vejamos o exemplo do número 6. Seus múltiplos são 0,6,12,18,24,30, etc. e seus divisores são 1,2,3 e 6. Logo percebemos porque Mínimo Múltiplo Comum e não em máximo, pois o conjunto dos múltiplos é infinito. E falamos Máximo divisor comum pois o conjunto dos divisores é finito, logo podemos encontrar um máximo valor em comum entre eles.

No estudo do M.M.C veremos suas propriedades, aplicação em cálculo com fração e como podemos encontrar este assunto no ENEM.

MMC

Um múltiplo positivo de um número é o produto desse número por qualquer outro número positivo. Dois ou mais números podem ter múltiplos comuns. O menor desses múltiplos comuns é o M.M.C. Com isso, denomina-se M.M.C de dois ou mais números inteiros o menor número inteiro que é múltiplo simultaneamente destes dois números.

Veja o exemplo:

Múltiplos de 4: 4,8,12,16,20,24,28,32,36,40,...

Múltiplos de 6: 6,12,18,24,30,36,,42,48,...

Logo, percebemos que os múltiplos em comum de 4 e 6 são: 12, 24,36, etc. Assim, o menor dos múltiplos em comum entre 4 e 6 é o 12. Uma forma de representar o menor múltiplo comum entre dois números é: M.M.C (4,6) = 12

Como calcular MMC

Agora vamos compreender como calcular o M.M.C através de dois métodos: comparação dos múltiplos e decomposição em fatores primos.

Método da comparação

Consiste em comparar os múltiplos dos números a serem comparados. Como no exemplo acima, determinamos os múltiplos de 4 logo em seguida os múltiplos de 6, comparamos estes múltiplos e percebemos que o menor entre eles é o 12. Logo o M.M.C (4,6) = 12.

Método da decomposição em fatores primos ou decomposição simultânea

Consiste em decompor todos os números em fatores primos ao mesmo tempo, num dispositivo como mostrado a seguir.

Logo o M.M.C (12,45) = 2².3².5 = 180. Este método pode ser usado com mais de dois números, veja o exemplo do cálculo do M.M.C (12,18,24):

Logo o M.M.C (12,18,24) = 2³.3² = 8.9 = 72.

Propriedades do MMC

O Mínimo Múltiplo comum entre dois ou mais números apresentam algumas propriedades veremos quais são agora:

O M.M.C de dois ou mais números primos entre si é o produto deles.

M.M.C (3,4), só existe um número que divide 3 e 4 logo, o

M.M.C (3,4) = 3.4 = 12.

M.M.C (99,100) = 99.100 = 9900

O M.M.C de dois ou mais números naturais onde o maior é múltiplo dos menores, o M.M.C é o maior.

M.M.C ( 4,8,16) = 16, pois o 16 é múltiplo de 8 e múltiplo de 4.

Logo ele é o M.M.C entre 4,8 e 16.

Qualquer múltiplo do M.M.C de dois ou mais números naturais também será múltiplo desses números.

Veja o exemplo a seguir:

M.M.C (3,4) = 12

Considerando os múltiplos de 12 temos:

M(12) = {0,12,24,36…}

Logo, estes números também são múltiplos de 3 e 4.

O Produto do M.M.C pelo M.D.C de dois números naturais é igual ao produto dos números.

Vale enfatizar que esta propriedade só é válida para dois números inteiros, enquanto as três anteriores para dois ou mais.

Vamos considerar os números inteiros 60 e 36. Logo o produto:

M.M.C (60,36) . M.D.C (60,36) = 60 .36

= 2² . 3 . 5 . 2².3²

= 2160

MMC em Frações

Em operações de soma e subtração com frações de denominadores diferentes temos a necessidade de igualar os denominadores para assim operarmos. Para igualar os denominadores utilizamos o M.M.C para encontrar o denominador comum para as frações: Vejamos um exemplo:

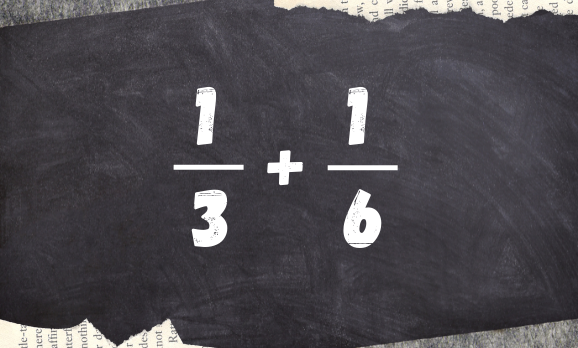
Logo, o M.M.C (3,6) nos dará um novo denominador. Podemos utilizar os métodos e as propriedades para determinação deste M.MC. Logo, o M.M.C (3,6) = 6

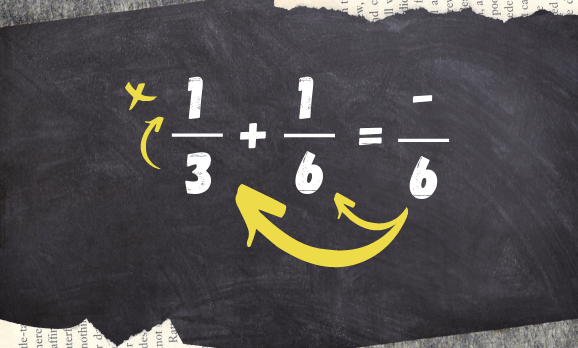
Denominador determinado, agora vamos ao numerador. Dividiremos o denominador em comum encontrado, pelos outros dois denominadores, e multiplicamos pelos respectivos numeradores:

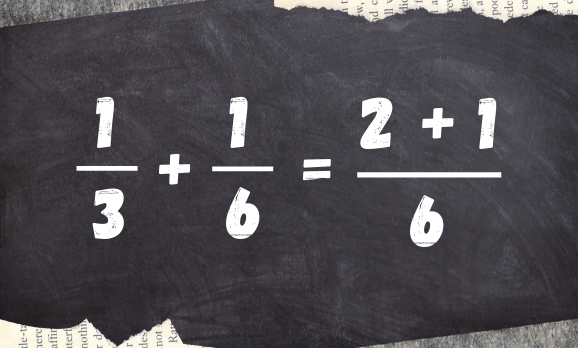
Vejamos em outro exemplo:

MMC no Enem

Este tópico de aritmética ou matemática básica tem sua carteirinha carimbada no ENEM. Constantemente vemos problemas de M.M.C nas provas anuais. Vejamos alguns exemplos:

(FMJ) Um grupo de 4 nadadores atravessa uma piscina, que tem 20 m de um lado a outro, com tempos individuais de 12 s, 15 s, 18 s e 25 s. Esses atletas iniciaram um treino, de um mesmo lado da piscina, atravessando-a de um lado para outro continuamente. Quando chegam a um lado da piscina, eles imediatamente passam a nadar em direção ao lado oposto. A primeira vez em que os quatro nadadores chegarem, ao mesmo tempo, em um mesmo lado da piscina, o nadador mais rápido terá nadado um total de:

A) 1.000 m.

B) 2.000 m.

C) 2.500 m.

D) 1.500 m.

E) 3.000 m.

Para resolução do problema vamos fazer o M.M.C (12,15,18,25):

12,15,18,25 | 2

6,15,9,25 | 2

3,15,9,25 | 3

1,5, 3, 25 | 3

1,5,1,25 | 5

1,1,1,5 | 5

1,1,1,1 \ 2².3².5² = 900

Se o nadador mais rápido nada 20 metros a cada 12 segundos, temos que:

900 : 12 = 75 voltas e 75 · 20 = 1500 metros

Os problemas que utilizam puramente M.M.C. para serem resolvidos, como o problema acima, sempre trazem a noção de ciclo, ou seja, algo que se repete de tempos em tempos ou que devemos realizar alguma ação repetidamente a cada período, metro, medição, determinada quantidade, etc.