MDC: Máximo Divisor Comum - O que é e suas propriedades

O Máximo Divisor Comum (M.D.C) entre dois ou mais números é o maior (Máximo) número que divide simultaneamente (comum) os dois ou mais números. Um número pode ter dois ou mais divisores, se for primo apresentará apenas dois divisores.

O M.D.C é uma comparação para encontrar o maior divisor entre dois ou mais algarismos. Como o conjunto dos divisores é finito, podemos encontrar o maior divisor, o que não acontece no M.M.C, pois os múltiplos de um número são infinitos, então encontramos o menor múltiplo comum. Estudaremos o que é o M.D.C., como calculamos, suas propriedades e aplicações no ENEM.

O que é MDC?

Máximo Divisor Comum (M.D.C) é o maior número que divide simultaneamente os valores a serem comparados. Vejamos alguns exemplos:

D(10) = 1,2,5,10

D(12) = 1,2,3,4,6,12

Logo percebemos que o maior valor que divide ao mesmo tempo o 10 e o 12 é o 2.

Logo o M.D.C (10,12) = 2

Como calcular o MDC

Estudaremos três métodos para o cálculo do M.D.C: o primeiro método é o da comparação, o segundo o algoritmo de Euclides e o terceiro, o método da decomposição em fatores primos.

Método da comparação

Vamos determinar o M.D.C (36,60)

D (36) = {1,2,3,4,6,9,12,18,36}

D (60) = {1,2,3,4,5,6,10,12,15,20,30,60}

M.D.C (36,60) = 12

Método das divisões sucessivas ou algoritmo de Euclides

1º Vamos desenhar uma malha e na linha do centro inserir os valores do maior para o menor:

2º Agora iremos realizar sucessivas divisões da esquerda para direita, com os números da linha central, o quociente vai para linha superior e o resto para a linha inferior:

3º O resto, 24 vamos inserir na linha central após o último valor, e seguiremos o processo:

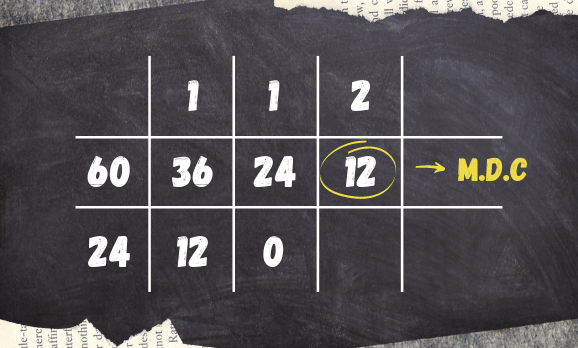
4º O processo finaliza quando encontramos o resto zero, logo o último valor encontrado é 12, então esse é o M.D.C.

Vejamos outro exemplo o M.D.C entre 10 e 12:

Método da decomposição em fatores primos

Para o terceiro método vamos utilizar a fatoração, ou seja, decomposição em fatores primos. Vejamos o M.D.C (36,60) através deste método.

60 = 2².3.5

36 = 2².3²

Portanto o M.D.C será o produto dos fatores primos comuns de menor expoente.

M.D.C (36,60) = 2².3 = 12

Vejamos outro exemplo: M.D.C (180,280,300)

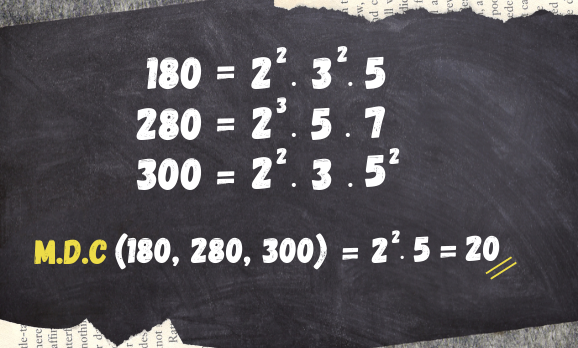
Propriedades do MDC

1ª Propriedade: se M.D.C de dois ou mais números é 1, então, estes números são primos entre si.

M.D.C (7,3) = 1

M.D.C( 10,11,12) = 1

M.D.C (11,4) = 1

2ª Propriedade: O M.D.C de dois ou mais números, onde o menor é divisor dos maiores, é o menor deles.

M.D.C (4,8) = 4

M.D.C (60,36,12) = 12

3ª Propriedade: Seja k,a_1,a_2,a_3,⋯ números naturais diferentes de zero:

MDC(ka_1,ka_2,ka_3…)=K.MDC(a_1,a_2,a_3,⋯)

Veja o exemplo a seguir:

MDC (180,280,300) = 20.MDC(9,14,15) = 20.1 = 20

4ª Propriedade: Seja a,b,c números naturais

MDC(a,b,c)=MDC(MDC(a,b),c)=MED(a,MDC(b,c))

Confira no exemplo:

MDC ( 60,48,36) = MDC(MDC(60,36), 48) = MDC (12,48) = 12

MDC no ENEM

O M.D.C pode ser encontrado no ENEM assim como o M.M.C de forma direta, para resolução de um problema, ou sendo um mecanismo usado em outro assunto, contudo necessário para a resolução do problema. Vejamos alguns problemas:

1) Uma empresa de logística é composta de três áreas: administrativa, operacional e vendedores. A área administrativa é composta de 30 funcionários, a operacional de 48 e a de vendedores com 36 pessoas. Ao final do ano, a empresa realiza uma integração entre as três áreas, de modo que todos os funcionários participem ativamente. As equipes devem conter o mesmo número de funcionários com o maior número possível. Determine quantos funcionários devem participar de cada equipe e o número possível de equipes.

Para a resolução deste problema utilizaremos o M.D.C (30,36,48), para assim sabermos com quantos participantes cada equipe ficará. Calcularemos o M.D.C (30,36,48), pelo método da decomposição:

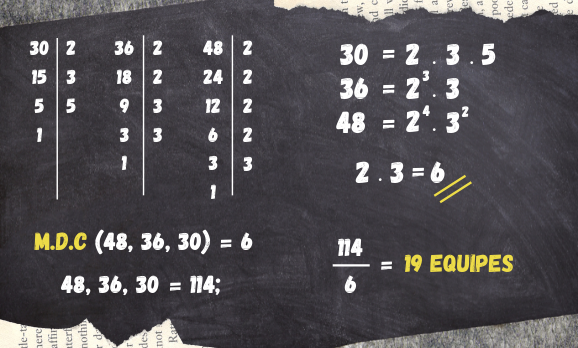
2) Uma indústria de tecidos fabrica retalhos de mesmo comprimento. Após realizarem os cortes necessários, verificou-se que duas peças restantes tinham as seguintes medidas: 156 centímetros e 234 centímetros. O gerente de produção, ao ser informado das medidas, deu a ordem para que o funcionário cortasse o pano em partes iguais e de maior comprimento possível. Como ele poderá resolver essa situação?

Para a resolução deste problema devemos encontrar o M.D.C, entre 156 e 254, pois esse valor será equivalente à medida do comprimento desejado. MDC (156,234), vamos resolver pelo algoritmo de Euclides:

MDC (156,234) = 78. Portanto, os retalhos podem ter 78cm de comprimento.