Juros Compostos: o que é, fórmula e como calcular

Os Juros compostos estão presentes em diversos eventos do cotidiano. Nas relações comerciais, nos descontos, atrasos de pagamentos, compras parceladas, investimentos e nas questões de matemática. Para quem faz parte das transações financeiras os juros podem ser bons ou indicar um prejuízo. Para conhecer bem esse conceito e aprender a calcular é importante dominar os conceitos que influenciam no seu cálculo, que são o capital, a taxa de juros, o tempo e o montante.

Ao comparar o conceito de juros simples com juros compostos conseguimos compreender que o primeiro é calculado em cima de um valor fixo inicial, já o segundo é calculado em cima do valor anterior, desta forma, os juros compostos terão sempre um maior crescimento em relação ao passar do tempo comparado aos juros simples.

Juros Compostos

É uma aplicação de juros sobre juros, ou seja, são juros aplicados ao que chamamos de montante de cada período, desse modo, os juros vão crescendo de acordo com o passar do tempo.

Esse modelo é preferido pelo sistema financeiro, pois oferta uma lucratividade melhor se comparado ao sistema de juros simples, que recaem apenas sobre o capital inicial, sendo fixo.

Fórmula

A fórmula utilizada para o cálculo de juros compostos é:

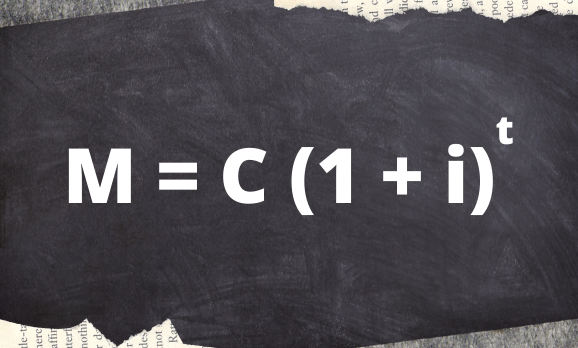
Onde,

J = Juros. É o valor de compensação para o rendimento. É o rendimento que se obtém quando se empresta dinheiro por um determinado período.

M = Montante. É o valor final da transação. O montante é calculado pela soma do capital com os juros — M = C + J.

C = Capital Inicial. É o primeiro valor investido. Conhecemos como capital o valor inicial da negociação, ou seja, ele é o valor de referência para calcularmos os juros com o passar do tempo.

i = Taxa de Juros. É a porcentagem cobrada em cima do capital a cada instante. Essa taxa pode ser ao dia (a.d.), ao mês (a.m.), ao bimestre (a.b.) ou ao ano (a.a.). A taxa de juros é uma porcentagem geralmente representada na forma percentual, porém, para calcular-se os juros compostos, é importante escrevê-la sempre na forma decimal.

T = Tempo. É o tempo em que o capital ficará aplicado. É importante que a taxa de juros (i) e o tempo (t) estejam sempre na mesma unidade de medida.

Como calcular

Saber utilizar a fórmula é primordial para o cálculo de juros compostos. Existem quatro variáveis (montante, capital, taxa de juros e tempo), os exercícios que trazem esse tema podem dar o valor de três delas e sempre pedir o cálculo da quarta variável, podendo ser qualquer uma delas. Por isso, o domínio de equações é fundamental para a resolução de questões que envolvem juros compostos.

Para calcular os juros, é necessário saber o capital (C) e montante (M), que são dados pela fórmula:

J = M-C

Nos problemas de juros compostos, pode ser pedido para se encontrar os juros ou montante, a taxa de juros ou tempo. Vamos analisar esses três casos:

Encontrando os juros e montante:

Exemplo: Um capital de R$1400 foi aplicado a juros compostos em um fundo de investimento que rende 7% a.a. Qual será o juros acumulado após 24 meses?

Solução:

C = 1400;

i = 7% a.a. = 0,007

t = 24 meses = 2 anos

M = C (1 + i) t

M = 1400 (1 + 0,07)²

M = 1400 (1,07)²

M = 1400 . 1,1449

M = 1602,86.

Para encontrar o juros, temos que:

J = M – C

1602,86 – 1400 = 202,86

Encontrando a taxa de juros:

Exemplo: Qual é a taxa de juros aplicada ao ano para que um capital de R$800 gere um juros de R$352 em dois anos?

Resolução: Dados: C = 800; t = 2 anos; J = 352.

Para encontrar a taxa, precisamos primeiro encontrar o montante. M = C + J 800 + 352 = 1152

Então: Transformando em porcentagem, temos: 20%.

Encontrando o tempo:

Exemplo: Quanto tempo um capital de R$1500 aplicado a juros compostos, com taxa de 10% a.a, leva para gerar um montante de R$1996,50?

Resolução: No caso em que precisamos encontrar o tempo iremos encontrar uma equação exponencial, pois t é uma potência. Para resolver podemos utilizar fatoração ou logaritmo. Nesse caso, o recomendado é utilizar uma calculadora, pois nem sempre se trata de um número inteiro, em vestibulares o valor do logaritmo ou da potência é dado na questão.

Dados: C = 1500 M = 1996,50 i = 10% = 0,01

Diferença entre juros simples e juros compostos

Como falamos anteriormente, nos juros simples, a taxa de juros incide sempre sobre o valor inicial. Nos juros compostos, a taxa de juros incide sempre sobre o valor anterior, o que acaba criando um montante muito mais expressivo.

Os juros simples utilizam uma fórmula diferente da apresentada para os juros compostos:

J = C . i . t

Para ilustrar essa diferença, vamos a analisar os seguintes exemplos: Se você aplica R$500 com juros simples de 10 % ao mês, então todo mês aquele capital renderá 10 % de R$500, ou seja, R$50, não importa o tempo que permanecer lá. O juros simples é comum para o atraso de contas, como de água e energia. A cada dia de atraso, a soma dá-se com um valor fixo calculado em cima da conta.

Já o juros compostos, pensando no mesmo valor e na mesma taxa, no primeiro mês, seu rendimento é calculado em cima do valor anterior. Por exemplo, no primeiro mês, os 10% serão calculados em cima dos R$500, gerando R$50 de juros e um montante de R$550.

No próximo mês, os 10 % serão calculados em cima do valor atual do montante, ou seja, 10 % de R$550, gerando um juros de R$55, e assim sucessivamente. Dessa forma, para investimentos, o juros composto é mais vantajoso. Ele é bastante comum exatamente nesse segmento de investimentos, como a poupança.

Comparando os dois sistemas, nesse caso, temos:

Podemos ainda trazer outras diferenças entres os dois sistemas:

Juros Simples

• Se somados ao capital e feito um gráfico, formaria uma reta. Ex: 1000, 1100, 1200,...
• São pagos mensal ou anualmente.

Juros Compostos

• Se somados ao capital e feito um gráfico formam uma curva ascendente. Ex: 1000, 1100, 1210,...
• São pagos apenas no vencimento.
• São pagos ao credor somente no vencimento.

Juros Compostos no Enem

(ENEM – 2018) Um contrato de empréstimo prevê que quando uma parcela é paga de forma antecipada, conceder-se-á uma redução de juros de acordo com o período de antecipação. Neste caso, paga-se o valor presente, que é o valor naquele momento, de uma quantia que deveria ser paga em uma data futura. Um valor presente P submetido a juros compostos com taxa i, por um período de tempo n, produz um valor futuro V determinado pela fórmula

Em um contrato de empréstimo com sessenta parcelas fixas mensais, de R$ 820,00, a uma taxa de juros de 1,32% ao mês, junto com a trigésima parcela será paga antecipadamente uma outra parcela, desde que o desconto seja superior a 25% do valor da parcela.

Utilize 0,2877 como aproximação parae 0,0131 como aproximação para ln (1,0132). A primeira das parcelas que poderá ser antecipada junto com a 30ª é a:

a) 56ª

b) 55ª

c) 52ª

d) 51ª

e) 45ª

Solução:

Na questão proposta, queremos descobrir qual a parcela que, aplicando a redução de juros ao pagar antecipadamente, o valor pago tenha um desconto superior 25%, ou seja:

Simplificando a fração (dividindo em cima e embaixo por 25), descobrindo que o valor a ser pago pela parcela antecipada deve ser:

A parcela antecipada corresponde ao valor futuro corrigido para o valor presente, ou seja, descontado os juros de 1,32% ao pagar essa parcela antes do prazo, isto é:

Onde n é igual ao período que será antecipado. Substituindo essa expressão na anterior, temos:

Como aparece 820 em ambos os lados da desigualdade, podemos simplificar, "cortando" esse valor:

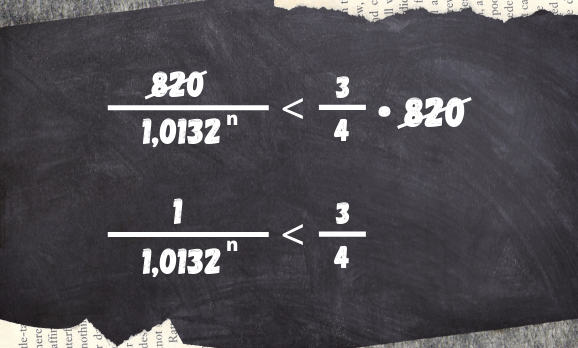
Podemos inverter as frações, tendo o cuidado de também inverter o sinal da desigualdade. Assim, nossa expressão fica:

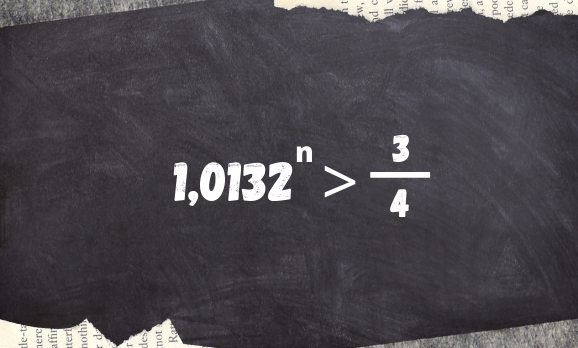
Observe que o valor que queremos descobrir está no expoente (n). Sendo assim, para resolver a inequação aplicaremos o logaritmo natural (ln) em ambos os lados da inequação, ou seja:

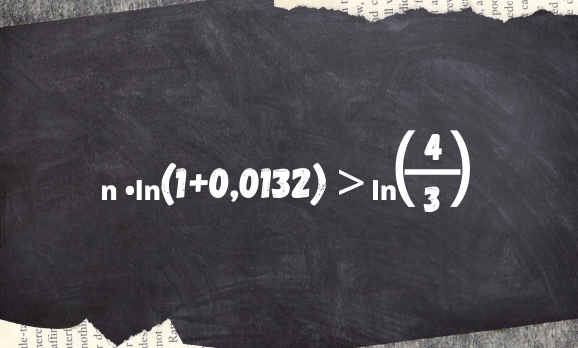
Agora, podemos substituir pelos valores indicados no enunciado e encontrar o valor do n:

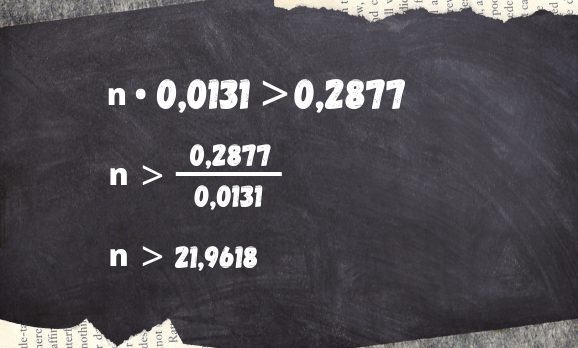
Como n deve ser maior que o valor encontrado, então teremos que antecipar 22 parcelas, ou seja, pagaremos a 30ª parcela junto com a 52ª ( 30 + 22 = 52). Alternativa: c) 52ª