Frações e números decimais: o que são, como usar e como cai no Enem
Publicado em: 13/10/2023Aqui veremos a descrição de números fracionários ou frações. Estes números pertencem à família dos números Racionais e possuem características particulares para as operações.
Tipos de frações
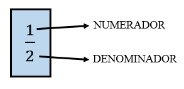
Frações são representações matemáticas que envolvem dois números. Nomeamos de numerador o número que se encontra na parte superior e de denominador, o número que está na parte inferior.
Fração própria
A fração própria caracteriza-se por ter o numerador menor do que o denominador. Ou seja, a fração própria é uma parte de um inteiro. Veja os exemplos a seguir:
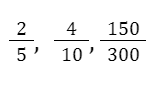
Fração imprópria
A fração imprópria caracteriza-se por ter o numerador maior do que o denominador. Ou seja, a fração imprópria é maior que um inteiro. Veja os exemplos a seguir:
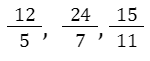
Fração mista

Fração equivalente
Algumas frações podem ser reduzidas. Veja os exemplos a seguir:
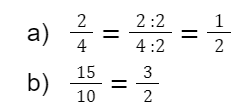
Nos exemplos acima, o numerador e o denominador são divisíveis por um divisor em comum, permitindo, assim, que toda a fração seja reduzida. Logo, no exemplo “a”, a fração dois quartos é equivalente à fração um meio. No exemplo b, a fração quinze décimos é equivalente à fração três meios.
Fração irredutível
As frações irredutíveis são aquelas onde nem o numerador e o denominador podem ser mais simplificados. Veja os exemplos:
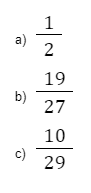
Números decimais
Outra forma de representarmos frações é utilizando números decimais. As casas decimais em um número fracionário são indicadas pela quantidade de zeros no denominador, veja o exemplo:
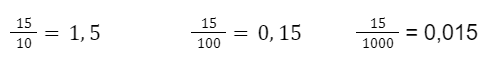
Operações com frações
Adição e subtração de fração com mesmo denominador.
Quando temos o mesmo denominador, e desejamos realizar soma ou subtração entre essas duas frações, repetimos o denominador e operamos apenas com o numerador. Veja os exemplos:
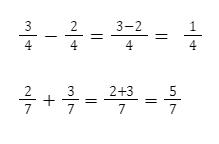
Adição e subtração com denominador diferente.
Para realizarmos soma ou subtração em frações com denominadores diferentes precisamos tornar o denominador das duas frações o mesmo. Este denominador em comum, será o Menor Múltiplo Comum dos denominadores. Veja o exemplo:
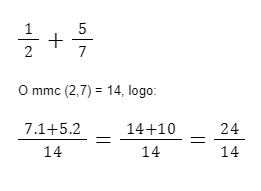
Multiplicação de fração
Na multiplicação entre frações multiplicamos o numerador pelo numerador e o denominador pelo denominador.
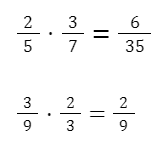
Divisão de fração
Na divisão entre frações repetimos a primeira fração e multiplicamos pelo inverso da segunda fração:
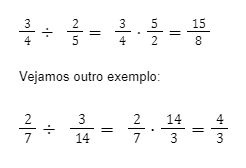
Operações com números decimais
Adição e subtração com números decimais.
As operações com números decimais de soma e subtração são realizadas da colocando vírgula embaixo de vírgula, vejamos:
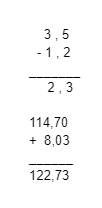
Multiplicação de Números decimais.
Ao multiplicarmos dois fatores decimais o produto terá a quantidade de casas decimais equivalente a soma das casas decimais dos fatores. Vejamos:
3,5 . 1,2 = 4,20
1,25 . 3,25 = 4,0625
Divisão de Números decimais.
O quociente entre dois números decimais pode ser obtido transformando os números decimais em frações. Vejamos:
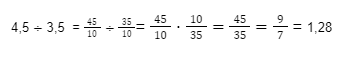
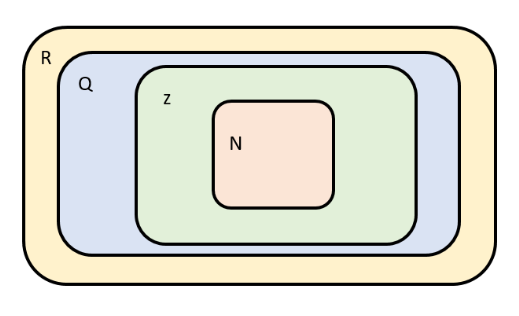
Conjuntos numéricos
Os números são agrupados em conjuntos numéricos, onde obedecem certas propriedades.
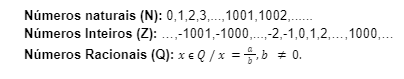
Frações e números decimais no Enem
(UFPE) A professora de Felipe recomendou que ele usasse a calculadora para fazer exercícios envolvendo operações com números decimais maiores que zero. Enquanto fazia os exercícios, algumas ideias foram surgindo na cabeça de Felipe:
I. O resultado de uma multiplicação entre dois desses números sempre é maior que cada um dos fatores;
II. O resultado de uma adição entre dois desses números sempre é maior que cada uma das parcelas;
III. O resultado de uma divisão entre dois desses números nunca será um número natural.
Assinale a alternativa em que as afirmações indicadas são verdadeiras:
a) II. b) III. c) I e III. d) I e II.
RESPOSTA: a
Apenas a afirmação II é verdadeira. O resultado de uma multiplicação entre dois desses números nem sempre é maior que cada um dos fatores; O resultado de uma divisão entre dois desses números pode ser um número natural.