Equação do 1° grau: o que é e como calcular

Alguns documentos antigos, como os papiros egípcios, traziam inúmeros e curiosos problemas matemáticos. “Uma quantidade, sua metade, seus dois terços, todos juntos são 26. Diga-me qual é essa quantidade?”. Historicamente, graças ao avanço na linguagem da matemática, hoje podemos resolver o problema acima com a equação. Vejamos:

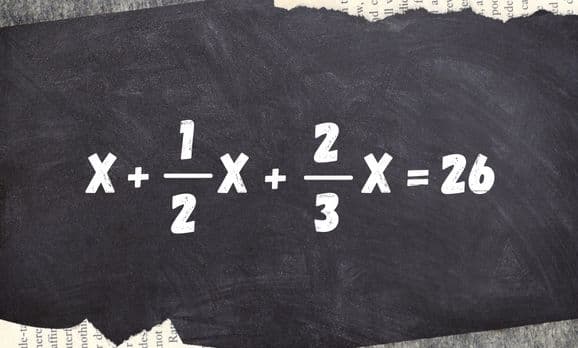
Nesta equação podemos encontrar algum valor para x, ou nenhum, o valor encontrado que satisfaz a equação denominamos raiz da equação. Por ter no máximo uma raiz denominamos esta equação de equação do primeiro grau. 

Perceba no exemplo acima que a variável, x, apresenta expoente 1. Isso caracteriza as equações do primeiro grau. Diferente das equações do segundo grau, onde a variável apresenta expoente 2. Por esse motivo, nomeamos ambas equações respectivamente como: equação polinomial do 1° grau e equação polinomial do 2° grau. 

O que é uma equação do 1° grau

 Equações que podem ser escritas como:

São denominadas equações polinomiais do primeiro grau. Vejamos alguns exemplos:

O objetivo é encontrarmos o valor de x (Incógnita ou variável), que satisfaça a equação.

Vejamos o exemplo: 

Ana recebeu 210 reais de mesada. Isso representa 4 vezes o que Victor recebeu somado a 10 reais. Qual o valor que Victor recebeu?

Para resolver este problema, pode-se fazer o caminho inverso. Subtrair 10 reais de 210 resultando em 200 reais, e agora, dividir 200 reais por 4, resultando em 50 reais. Eis o valor da mesada de Victor. Contudo, podemos representar o problema por meio de uma equação:

4x + 10 = 210

Como resolver uma equação do 1° grau

Resolver uma equação consiste em encontrar o valor da incógnita que torna a sentença verdadeira, ou seja, encontrar a solução ou a raiz da equação. Em toda equação polinomial podemos visualizar o primeiro membro da equação e o segundo membro.

1º Passo: Deixar no primeiro membro todos os termos que apresentem a variável, os termos que não apresentam a variável vão para o 2º membro da equação. Subtraindo 10 de cada lado temos:

4x + 10 - 10 = 210 - 10

4x = 200

2º Passo: Ao ser isolado no primeiro membro, a variável pode ainda está sendo multiplicada ou dividida por algum valor. Caso isso aconteça, precisamos deixar apenas a variável. Para isto vamos dividir por quatro ambos os membros. 

4x / 4 = 200/4

x = 50, este é o único valor para x que satisfaz a equação. 

Generalizando o processo de encontrar a raiz da equação do 1º grau temos:

Propriedade fundamental das equações

Como vimos acima, a resolução de uma equação polinomial do primeiro grau tem uma semelhança com uma balança de pratos em posição de equilíbrio. Assim como em uma balança de pratos, para que haja o equilíbrio deve haver as mesmas quantidades de massa nos dois pratos.

Para termos uma igualdade na equação polinomial do primeiro grau, temos que realizar as mesmas operações em ambos os membros da equação. O que garante o equilíbrio na balança é a igualdade. Vejamos  o exemplo a seguir:

x + 1 = 2 

Para chegarmos a resolução deste problema operamos nos dois membros. Subtraímos 1, veja:

x + 1 - 1 = 2 -1

Logo o valor de x é:

x = 1

Ter ciência desta propriedade nos previne de cometer erros como estes:

Ao passar o 3 multiplicando o 27 ignoramos o fato desta operação não ter sido aplicada em todo o primeiro membro:

Equação do 1° grau no Enem

Como vimos, a equação do primeiro grau nos auxilia muito para resolução de vários problemas na álgebra. No ENEM podemos ter um problema envolvendo o uso direto da resolução da Equação Polinomial do 1º grau, ou, podemos encontrar problemas que utilizaremos a equação para nos auxiliar na resolução.

Questão com equação do 1° grau no Enem de 2009

Um grupo de 50 pessoas fez um orçamento inicial para organizar uma festa, que seria dividido entre elas em cotas iguais. Verificou-se ao final que, para arcar com todas as despesas, faltavam R$ 510,00, e que 5 novas pessoas haviam ingressado no grupo. No acerto foi decidido que a despesa total seria dividida em partes iguais pelas 55 pessoas. Quem não havia ainda contribuído pagaria a sua parte, e cada uma das 50 pessoas do grupo inicial deveria contribuir com mais R$ 7,00.

De acordo com essas informações, qual foi o valor da cota calculada no acerto final para cada uma das 55 pessoas?

a) R$ 14,00.

b) R$ 17,00.

c) R$ 22,00.

d) R$ 32,00.

e) R$ 57,00.

Resolução Podemos modelar o problema com a seguinte equação:

(50 · 7) + (5 · x) = 510

350 + 5x = 510

5x = 510 – 350

5x = 160

x = 32

Portanto, cada um pagou o valor total de R$ 32,00. Logo, a alternativa correta é a letra d.